Verifiable Natural Language to Linear Temporal Logic Translation: A Benchmark Dataset and Evaluation Suite

Empirical evaluation of state-of-the-art natural-language (NL) to temporal-logic (TL) translation systems reveals near-perfect performance on existing benchmarks. However, current studies measure only the accuracy of the translation of NL logic into formal TL, ignoring a system's capacity to ground atomic propositions into new scenarios or environments. This is a critical feature, necessary for the verification of resulting formulas in a concrete state space. Consequently, most NL-to-TL translation frameworks propose their own bespoke dataset in which the correct grounding is known a-priori, inflating performance metrics and neglecting the need for extensible, domain-general systems. In this paper, we introduce the Verifiable Linear Temporal Logic Benchmark ( VLTL-Bench), a unifying benchmark that measures verification and verifiability of automated NL-to-LTL translation. The dataset consists of three unique state spaces and thousands of diverse natural language specifications and corresponding formal specifications in temporal logic. Moreover, the benchmark contains sample traces to validate the temporal logic expressions. While the benchmark directly supports end-to-end evaluation, we observe that many frameworks decompose the process into i) lifting, ii) grounding, iii) translation, and iv) verification. The benchmark provides ground truths after each of these steps to enable researches to improve and evaluate different substeps of the overall problem. To encourage methodologically sound advances in verifiable NL-to-LTL translation approaches, we release VLTL-Bench here: https://www.kaggle.com/datasets/dubascudes/vltl bench.

Integrated Decision Gradients: Compute Your Attributions Where the Model Makes Its Decision

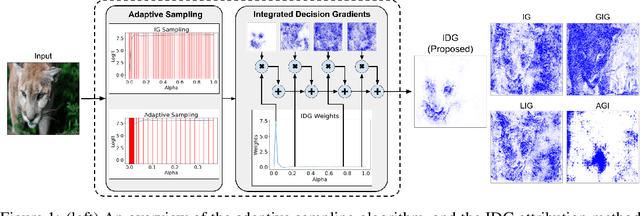
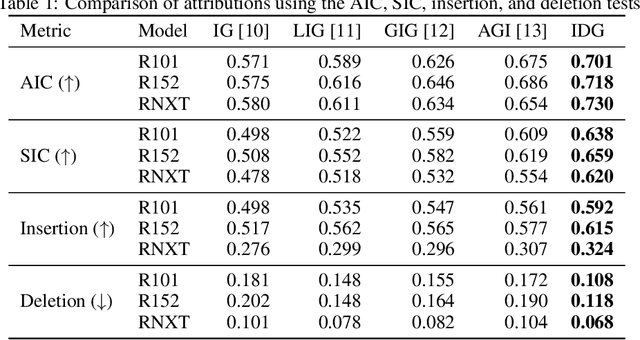
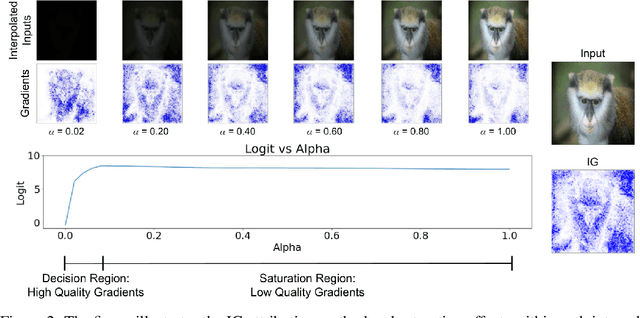
Attribution algorithms are frequently employed to explain the decisions of neural network models. Integrated Gradients (IG) is an influential attribution method due to its strong axiomatic foundation. The algorithm is based on integrating the gradients along a path from a reference image to the input image. Unfortunately, it can be observed that gradients computed from regions where the output logit changes minimally along the path provide poor explanations for the model decision, which is called the saturation effect problem. In this paper, we propose an attribution algorithm called integrated decision gradients (IDG). The algorithm focuses on integrating gradients from the region of the path where the model makes its decision, i.e., the portion of the path where the output logit rapidly transitions from zero to its final value. This is practically realized by scaling each gradient by the derivative of the output logit with respect to the path. The algorithm thereby provides a principled solution to the saturation problem. Additionally, we minimize the errors within the Riemann sum approximation of the path integral by utilizing non-uniform subdivisions determined by adaptive sampling. In the evaluation on ImageNet, it is demonstrated that IDG outperforms IG, left-IG, guided IG, and adversarial gradient integration both qualitatively and quantitatively using standard insertion and deletion metrics across three common models.