A deep mixture density network for outlier-corrected interpolation of crowd-sourced weather data

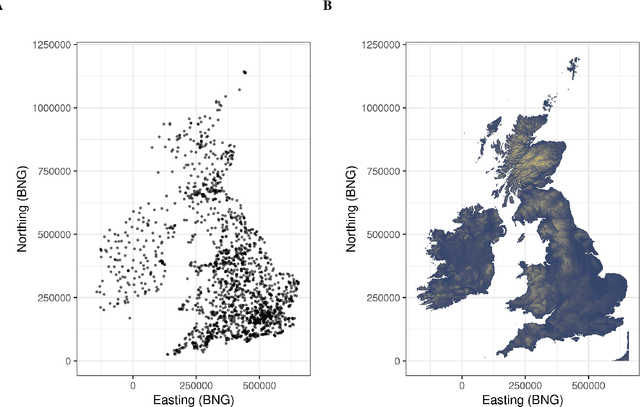
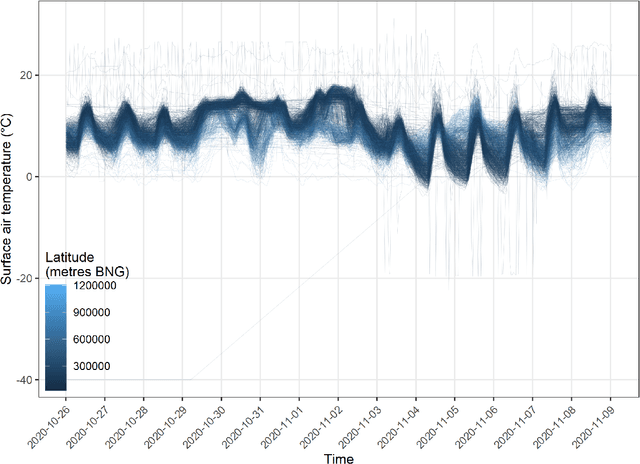
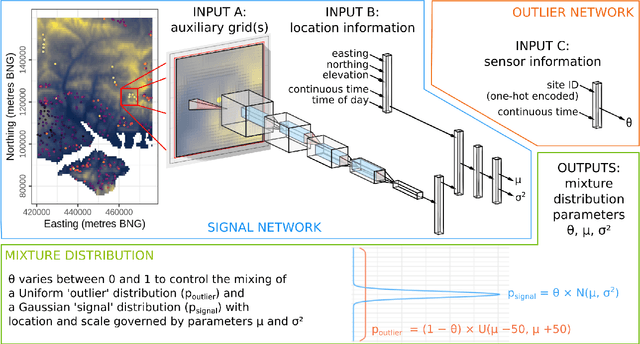
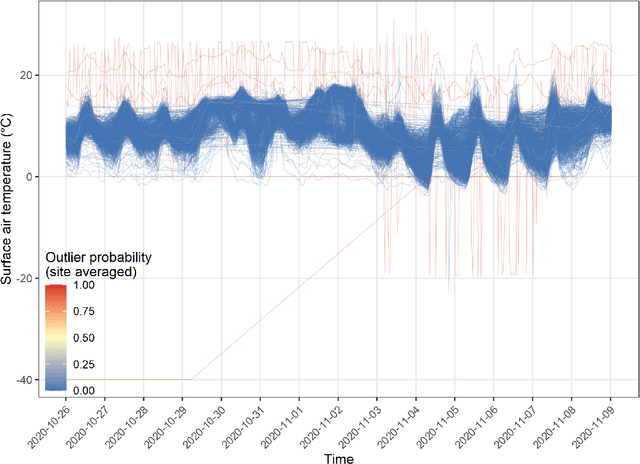
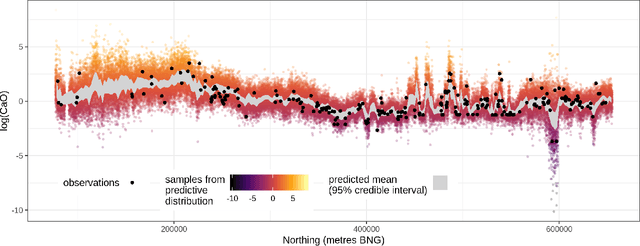
As the costs of sensors and associated IT infrastructure decreases - as exemplified by the Internet of Things - increasing volumes of observational data are becoming available for use by environmental scientists. However, as the number of available observation sites increases, so too does the opportunity for data quality issues to emerge, particularly given that many of these sensors do not have the benefit of official maintenance teams. To realise the value of crowd sourced 'Internet of Things' type observations for environmental modelling, we require approaches that can automate the detection of outliers during the data modelling process so that they do not contaminate the true distribution of the phenomena of interest. To this end, here we present a Bayesian deep learning approach for spatio-temporal modelling of environmental variables with automatic outlier detection. Our approach implements a Gaussian-uniform mixture density network whose dual purposes - modelling the phenomenon of interest, and learning to classify and ignore outliers - are achieved simultaneously, each by specifically designed branches of our neural network. For our example application, we use the Met Office's Weather Observation Website data, an archive of observations from around 1900 privately run and unofficial weather stations across the British Isles. Using data on surface air temperature, we demonstrate how our deep mixture model approach enables the modelling of a highly skilled spatio-temporal temperature distribution without contamination from spurious observations. We hope that adoption of our approach will help unlock the potential of incorporating a wider range of observation sources, including from crowd sourcing, into future environmental models.

Bayesian deep learning for mapping via auxiliary information: a new era for geostatistics?

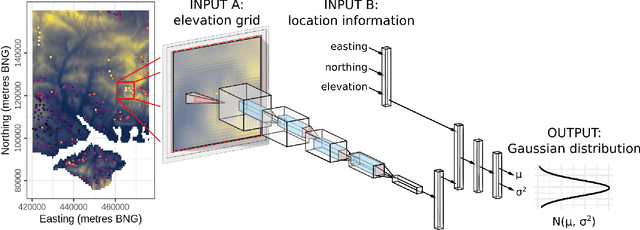
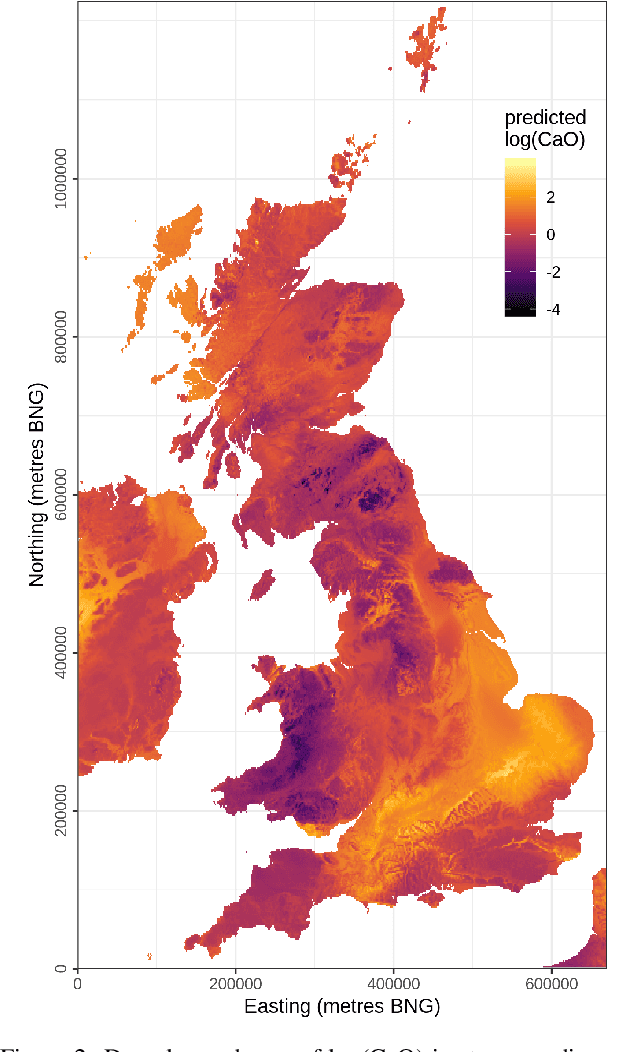
For geospatial modelling and mapping tasks, variants of kriging - the spatial interpolation technique developed by South African mining engineer Danie Krige - have long been regarded as the established geostatistical methods. However, kriging and its variants (such as regression kriging, in which auxiliary variables or derivatives of these are included as covariates) are relatively restrictive models and lack capabilities that have been afforded to us in the last decade by deep neural networks. Principal among these is feature learning - the ability to learn filters to recognise task-specific patterns in gridded data such as images. Here we demonstrate the power of feature learning in a geostatistical context, by showing how deep neural networks can automatically learn the complex relationships between point-sampled target variables and gridded auxiliary variables (such as those provided by remote sensing), and in doing so produce detailed maps of chosen target variables. At the same time, in order to cater for the needs of decision makers who require well-calibrated probabilities, we obtain uncertainty estimates via a Bayesian approximation known as Monte Carlo dropout. In our example, we produce a national-scale probabilistic geochemical map from point-sampled assay data, with auxiliary information provided by a terrain elevation grid. Unlike traditional geostatistical approaches, auxiliary variable grids are fed into our deep neural network raw. There is no need to provide terrain derivatives (e.g. slope angles, roughness, etc) because the deep neural network is capable of learning these and arbitrarily more complex derivatives as necessary to maximise predictive performance. We hope our results will raise awareness of the suitability of Bayesian deep learning - and its feature learning capabilities - for large-scale geostatistical applications where uncertainty matters.

Deep covariate-learning: optimising information extraction from terrain texture for geostatistical modelling applications

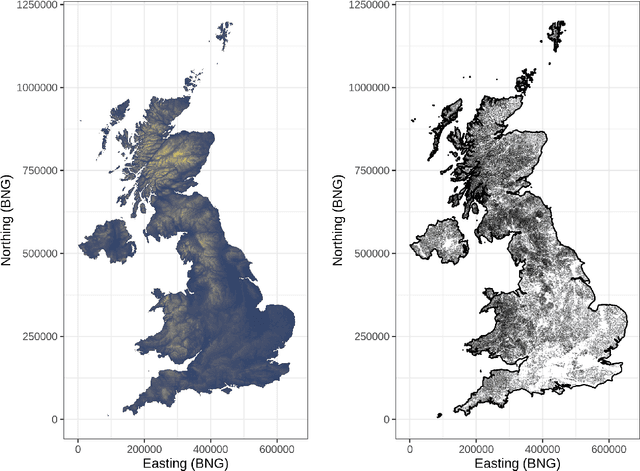
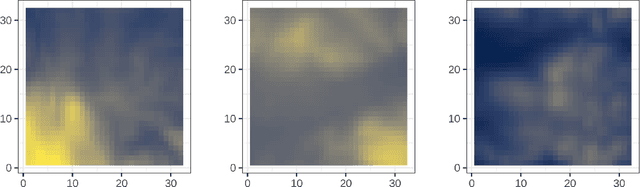
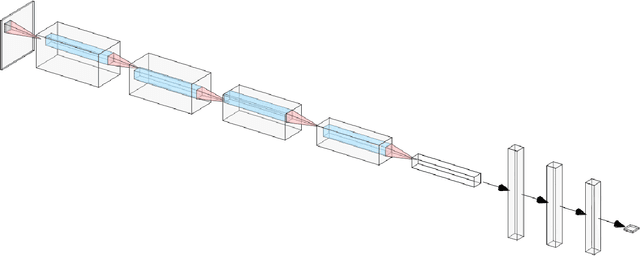
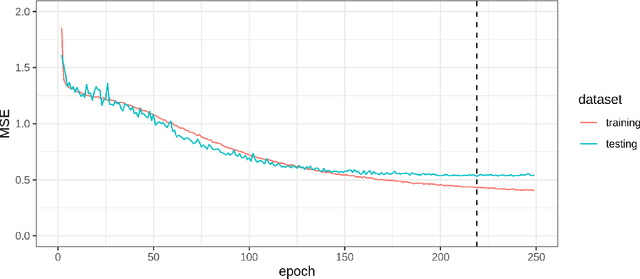
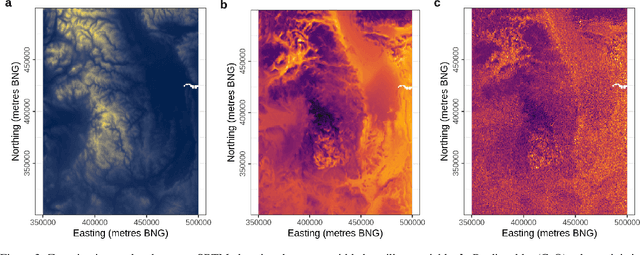
Where data is available, it is desirable in geostatistical modelling to make use of additional covariates, for example terrain data, in order to improve prediction accuracy in the modelling task. While elevation itself may be important, additional explanatory power for any given problem can be sought (but not necessarily found) by filtering digital elevation models to extract higher-order derivatives such as slope angles, curvatures, and roughness. In essence, it would be beneficial to extract as much task-relevant information as possible from the elevation grid. However, given the complexities of the natural world, chance dictates that the use of 'off-the-shelf' filters is unlikely to derive covariates that provide strong explanatory power to the target variable at hand, and any attempt to manually design informative covariates is likely to be a trial-and-error process -- not optimal. In this paper we present a solution to this problem in the form of a deep learning approach to automatically deriving optimal task-specific terrain texture covariates from a standard SRTM 90m gridded digital elevation model (DEM). For our target variables we use point-sampled geochemical data from the British Geological Survey: concentrations of potassium, calcium and arsenic in stream sediments. We find that our deep learning approach produces covariates for geostatistical modelling that have surprisingly strong explanatory power on their own, with R-squared values around 0.6 for all three elements (with arsenic on the log scale). These results are achieved without the neural network being provided with easting, northing, or absolute elevation as inputs, and purely reflect the capacity of our deep neural network to extract task-specific information from terrain texture. We hope that these results will inspire further investigation into the capabilities of deep learning within geostatistical applications.

A framework for probabilistic weather forecast post-processing across models and lead times using machine learning

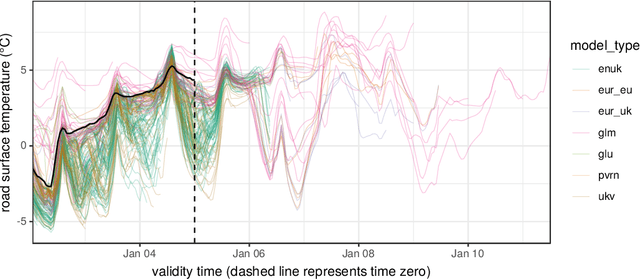
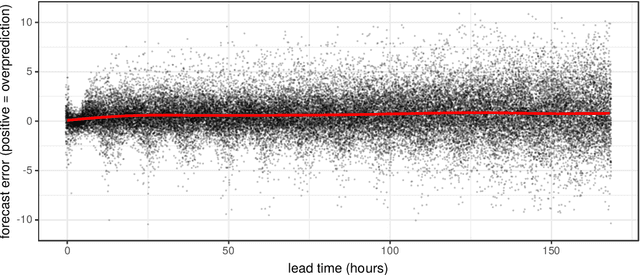
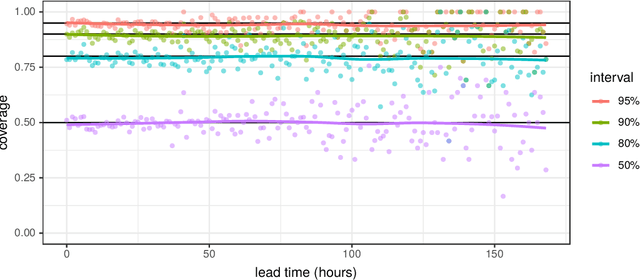
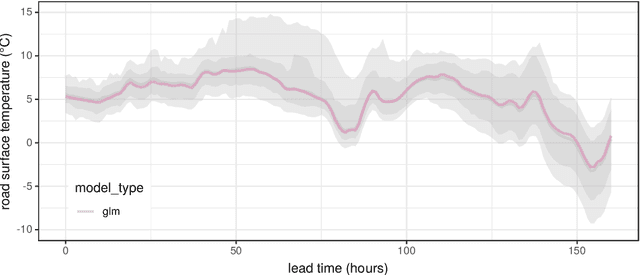
Forecasting the weather is an increasingly data intensive exercise. Numerical Weather Prediction (NWP) models are becoming more complex, with higher resolutions, and there are increasing numbers of different models in operation around the world. While the forecasting skill of NWP models continues to improve, the number and complexity of these models poses a new challenge for the operational meteorologist: how should the information from all available models, each with their own unique biases and limitations, be combined in order to provide stakeholders with well-calibrated probabilistic forecasts to use in decision making? In this paper, we use a road surface temperature forecasting example to demonstrate a three-stage framework that uses machine learning to bridge the gap between sets of separate forecasts from NWP models and the 'ideal' forecast for decision support: probabilities of future weather outcomes. First, we use Quantile Regression Forests to learn the error profile of each numerical model, and use these to apply empirically-derived probability distributions to forecasts. Second, we combine these probabilistic forecasts using quantile averaging. Third, we interpolate between the aggregate quantiles in order to generate a full predictive distribution, which we demonstrate has properties suitable for decision support. Our results suggest that this three stage approach provides an effective and operationally viable framework for the cohesive post-processing of weather forecasts across multiple models and lead times in order to produce well-calibrated probabilistic forecasts.