Changpeng Shao
Quantum algorithms for learning graphs and beyond
Nov 17, 2020
Abstract:We study the problem of learning an unknown graph provided via an oracle using a quantum algorithm. We consider three query models. In the first model ("OR queries"), the oracle returns whether a given subset of the vertices contains any edges. In the second ("parity queries"), the oracle returns the parity of the number of edges in a subset. In the third model, we are given copies of the graph state corresponding to the graph. We give quantum algorithms that achieve speedups over the best possible classical algorithms in the OR and parity query models, for some families of graphs, and give quantum algorithms in the graph state model whose complexity is similar to the parity query model. For some parameter regimes, the speedups can be exponential in the parity query model. On the other hand, without any promise on the graph, no speedup is possible in the OR query model. A main technique we use is the quantum algorithm for solving the combinatorial group testing problem, for which a query-efficient quantum algorithm was given by Belovs. Here we additionally give a time-efficient quantum algorithm for this problem, based on the algorithm of Ambainis et al.\ for a "gapped" version of the group testing problem. We also give simple time-efficient quantum algorithms based on Fourier sampling and amplitude amplification for learning the exact-half and majority functions, which almost match the optimal complexity of Belovs' algorithms.
Quantum algorithms for spectral sums
Nov 12, 2020
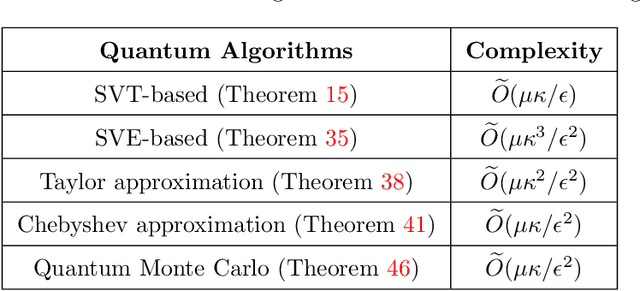
Abstract:We propose and analyze new quantum algorithms for estimating the most common spectral sums of symmetric positive definite (SPD) matrices. For a function $f$ and a matrix $A \in \mathbb{R}^{n\times n}$, the spectral sum is defined as $S_f(A) :=\text{Tr}[f(A)] = \sum_j f(\lambda_j)$, where $\lambda_j$ are the eigenvalues. Examples of spectral sums are the von Neumann entropy, the trace of inverse, the log-determinant, and the Schatten-$p$ norm, where the latter does not require the matrix to be SPD. The fastest classical randomized algorithms estimate these quantities have a runtime that depends at least linearly on the number of nonzero components of the matrix. Assuming quantum access to the matrix, our algorithms are sub-linear in the matrix size, and depend at most quadratically on other quantities, like the condition number and the approximation error, and thus can compete with most of the randomized and distributed classical algorithms proposed in recent literature. These algorithms can be used as subroutines for solving many practical problems, for which the estimation of a spectral sum often represents a computational bottleneck.
A simple approach to design quantum neural networks and its applications to kernel-learning methods
Oct 19, 2019



Abstract:We give an explicit simple method to build quantum neural networks (QNNs) to solve classification problems. Besides the input (state preparation) and output (amplitude estimation), it has one hidden layer which uses a tensor product of $\log M$ two-dimensional rotations to introduce $\log M$ weights. Here $M$ is the number of training samples. We also have an efficient method to prepare the quantum states of the training samples. By the quantum-classical hybrid method or the variational method, the training algorithm of this QNN is easy to accomplish in a quantum computer. The idea is inspired by the kernel methods and the radial basis function (RBF) networks. In turn, the construction of QNN provides new findings in the design of RBF networks. As an application, we introduce a quantum-inspired RBF network, in which the number of weight parameters is $\log M$. Numerical tests indicate that the performance of this neural network in solving classification problems improves when $M$ increases. Since using exponentially fewer parameters, more advanced optimization methods (e.g. Newton's method) can be used to train this network. Finally, about the convex optimization problem to train support vector machines, we use a similar idea to reduce the number of variables, which equals $M$, to $\log M$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge