Quantum algorithms for spectral sums
Paper and Code
Nov 12, 2020
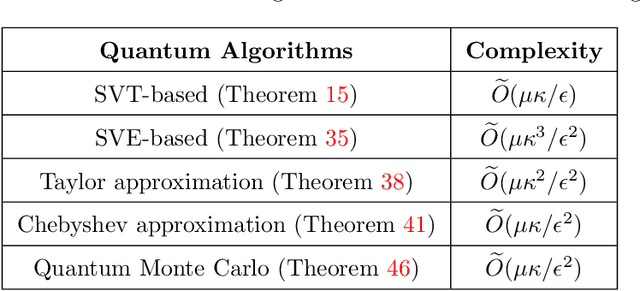
We propose and analyze new quantum algorithms for estimating the most common spectral sums of symmetric positive definite (SPD) matrices. For a function $f$ and a matrix $A \in \mathbb{R}^{n\times n}$, the spectral sum is defined as $S_f(A) :=\text{Tr}[f(A)] = \sum_j f(\lambda_j)$, where $\lambda_j$ are the eigenvalues. Examples of spectral sums are the von Neumann entropy, the trace of inverse, the log-determinant, and the Schatten-$p$ norm, where the latter does not require the matrix to be SPD. The fastest classical randomized algorithms estimate these quantities have a runtime that depends at least linearly on the number of nonzero components of the matrix. Assuming quantum access to the matrix, our algorithms are sub-linear in the matrix size, and depend at most quadratically on other quantities, like the condition number and the approximation error, and thus can compete with most of the randomized and distributed classical algorithms proposed in recent literature. These algorithms can be used as subroutines for solving many practical problems, for which the estimation of a spectral sum often represents a computational bottleneck.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge