Identifying treatment response subgroups in observational time-to-event data

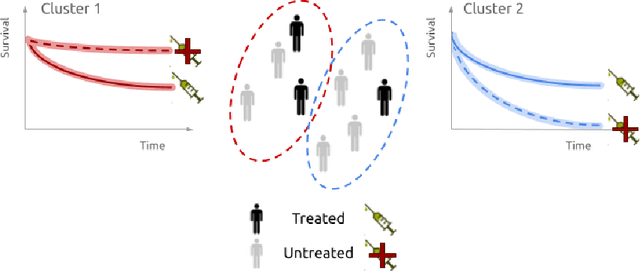
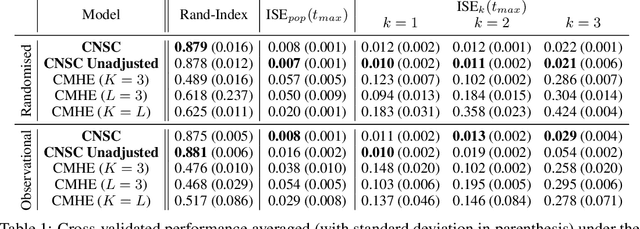
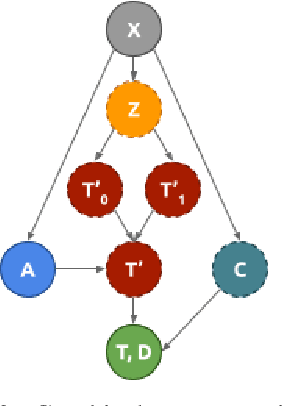
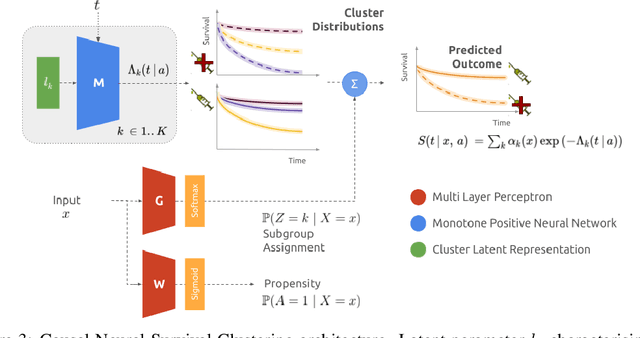
Identifying patient subgroups with different treatment responses is an important task to inform medical recommendations, guidelines, and the design of future clinical trials. Existing approaches for subgroup analysis primarily focus on Randomised Controlled Trials (RCTs), in which treatment assignment is randomised. Furthermore, the patient cohort of an RCT is often constrained by cost, and is not representative of the heterogeneity of patients likely to receive treatment in real-world clinical practice. Therefore, when applied to observational studies, such approaches suffer from significant statistical biases because of the non-randomisation of treatment. Our work introduces a novel, outcome-guided method for identifying treatment response subgroups in observational studies. Our approach assigns each patient to a subgroup associated with two time-to-event distributions: one under treatment and one under control regime. It hence positions itself in between individualised and average treatment effect estimation. The assumptions of our model result in a simple correction of the statistical bias from treatment non-randomisation through inverse propensity weighting. In experiments, our approach significantly outperforms the current state-of-the-art method for outcome-guided subgroup analysis in both randomised and observational treatment regimes.

Neural Fine-Gray: Monotonic neural networks for competing risks

Time-to-event modelling, known as survival analysis, differs from standard regression as it addresses censoring in patients who do not experience the event of interest. Despite competitive performances in tackling this problem, machine learning methods often ignore other competing risks that preclude the event of interest. This practice biases the survival estimation. Extensions to address this challenge often rely on parametric assumptions or numerical estimations leading to sub-optimal survival approximations. This paper leverages constrained monotonic neural networks to model each competing survival distribution. This modelling choice ensures the exact likelihood maximisation at a reduced computational cost by using automatic differentiation. The effectiveness of the solution is demonstrated on one synthetic and three medical datasets. Finally, we discuss the implications of considering competing risks when developing risk scores for medical practice.