Characterizing the Accuracy - Efficiency Trade-off of Low-rank Decomposition in Language Models

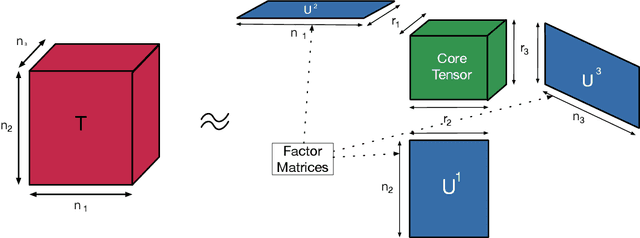
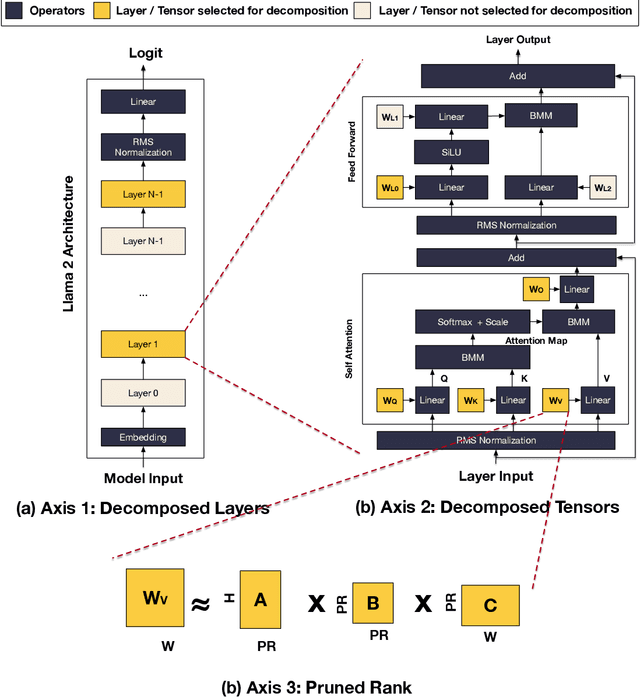
Large language models (LLMs) have emerged and presented their general problem-solving capabilities with one model. However, the model size has increased dramatically with billions of parameters to enable such broad problem-solving capabilities. In addition, due to the dominance of matrix-matrix and matrix-vector multiplications in LLMs, the compute-to-model size ratio is significantly lower than that of CNNs. This shift pushes LLMs from a computation-bound regime to a memory-bound regime. Therefore, optimizing the memory footprint and traffic is an important optimization direction for LLMs today. Model compression methods such as quantization and parameter pruning have been actively explored for achieving the memory footprint and traffic optimization. However, the accuracy-efficiency trade-off of rank pruning for LLMs is not well-understood yet. Therefore, we characterize the accuracy-efficiency trade-off of a low-rank decomposition method, specifically Tucker decomposition, on recent language models, including an open-source LLM, Llama 2. We formalize the low-rank decomposition design space and show that the decomposition design space is enormous (e.g., O($2^{37}$) for Llama2-7B). To navigate such a vast design space, we formulate the design space and perform thorough case studies of accuracy-efficiency trade-offs using six widely used LLM benchmarks on BERT and Llama 2 models. Our results show that we can achieve a 9\% model size reduction with minimal accuracy drops, which range from 4\%p to 10\%p, depending on the difficulty of the benchmark, without any retraining to recover accuracy after decomposition. The results show that low-rank decomposition can be a promising direction for LLM-based applications that require real-time service in scale (e.g., AI agent assist and real-time coding assistant), where the latency is as important as the model accuracy.