Learning complex dependency structure of gene regulatory networks from high dimensional micro-array data with Gaussian Bayesian networks

Gene expression datasets consist of thousand of genes with relatively small samplesizes (i.e. are large-$p$-small-$n$). Moreover, dependencies of various orders co-exist in the datasets. In the Undirected probabilistic Graphical Model (UGM) framework the Glasso algorithm has been proposed to deal with high dimensional micro-array datasets forcing sparsity. Also, modifications of the default Glasso algorithm are developed to overcome the problem of complex interaction structure. In this work we advocate the use of a simple score-based Hill Climbing algorithm (HC) that learns Gaussian Bayesian Networks (BNs) leaning on Directed Acyclic Graphs (DAGs). We compare HC with Glasso and its modifications in the UGM framework on their capability to reconstruct GRNs from micro-array data belonging to the Escherichia Coli genome. We benefit from the analytical properties of the Joint Probability Density (JPD) function on which both directed and undirected PGMs build to convert DAGs to UGMs. We conclude that dependencies in complex data are learned best by the HC algorithm, presenting them most accurately and efficiently, simultaneously modelling strong local and weaker but significant global connections coexisting in the gene expression dataset. The HC algorithm adapts intrinsically to the complex dependency structure of the dataset, without forcing a specific structure in advance. On the contrary, Glasso and modifications model unnecessary dependencies at the expense of the probabilistic information in the network and of a structural bias in the JPD function that can only be relieved including many parameters.

Who Learns Better Bayesian Network Structures: Constraint-Based, Score-based or Hybrid Algorithms?

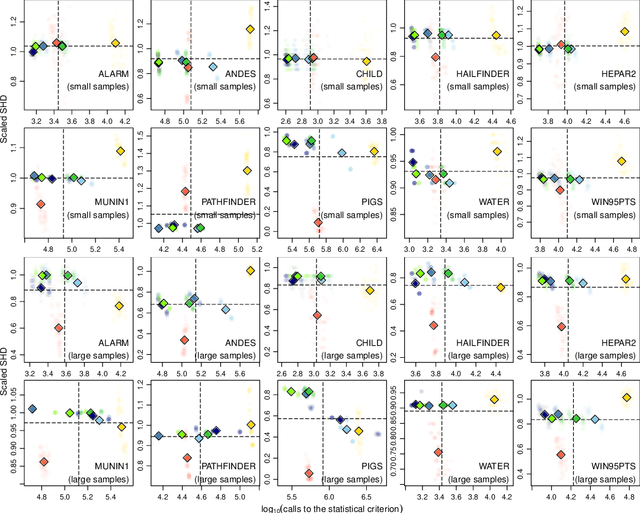
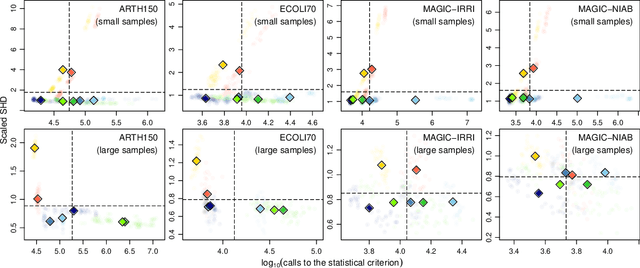
The literature groups algorithms to learn the structure of Bayesian networks from data in three separate classes: constraint-based algorithms, which use conditional independence tests to learn the dependence structure of the data; score-based algorithms, which use goodness-of-fit scores as objective functions to maximise; and hybrid algorithms that combine both approaches. Famously, Cowell (2001) showed that algorithms in the first two classes learn the same structures when the topological ordering of the network is known and we use entropy to assess conditional independence and goodness of fit. In this paper we address the complementary question: how do these classes of algorithms perform outside of the assumptions above? We approach this question by recognising that structure learning is defined by the combination of a statistical criterion and an algorithm that determines how the criterion is applied to the data. Removing the confounding effect of different choices for the statistical criterion, we find using both simulated and real-world data that constraint-based algorithms do not appear to be more efficient or more sensitive to errors than score-based algorithms; and that hybrid algorithms are not faster or more accurate than constraint-based algorithms. This suggests that commonly held beliefs on structure learning in the literature are strongly influenced by the choice of particular statistical criteria rather than just properties of the algorithms themselves.