An Interleaving Semantics of the Timed Concurrent Language for Argumentation to Model Debates and Dialogue Games

Time is a crucial factor in modelling dynamic behaviours of intelligent agents: activities have a determined temporal duration in a real-world environment, and previous actions influence agents' behaviour. In this paper, we propose a language for modelling concurrent interaction between agents that also allows the specification of temporal intervals in which particular actions occur. Such a language exploits a timed version of Abstract Argumentation Frameworks to realise a shared memory used by the agents to communicate and reason on the acceptability of their beliefs with respect to a given time interval. An interleaving model on a single processor is used for basic computation steps, with maximum parallelism for time elapsing. Following this approach, only one of the enabled agents is executed at each moment. To demonstrate the capabilities of language, we also show how it can be used to model interactions such as debates and dialogue games taking place between intelligent agents. Lastly, we present an implementation of the language that can be accessed via a web interface. Under consideration in Theory and Practice of Logic Programming (TPLP).

Implementing Ranking-Based Semantics in ConArg: a Preliminary Report

ConArg is a suite of tools that offers a wide series of applications for dealing with argumentation problems. In this work, we present the advances we made in implementing a ranking-based semantics, based on computational choice power indexes, within ConArg. Such kind of semantics represents a method for sorting the arguments of an abstract argumentation framework, according to some preference relation. The ranking-based semantics we implement relies on Shapley, Banzhaf, Deegan-Packel and Johnston power index, transferring well know properties from computational social choice to argumentation framework ranking-based semantics.

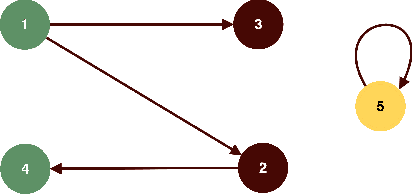
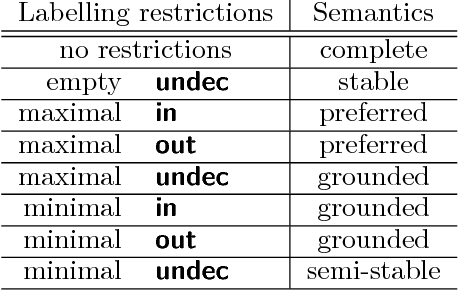
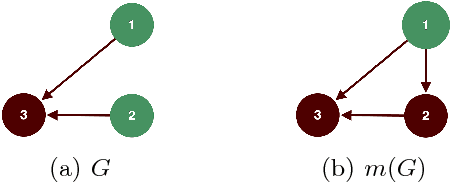
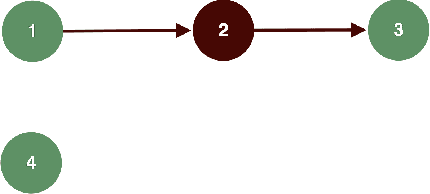
On Looking for Local Expansion Invariants in Argumentation Semantics: a Preliminary Report

We study invariant local expansion operators for conflict-free and admissible sets in Abstract Argumentation Frameworks (AFs). Such operators are directly applied on AFs, and are invariant with respect to a chosen "semantics" (that is w.r.t. each of the conflict free/admissible set of arguments). Accordingly, we derive a definition of robustness for AFs in terms of the number of times such operators can be applied without producing any change in the chosen semantics.

A Matrix Approach for Weighted Argumentation Frameworks: a Preliminary Report

The assignment of weights to attacks in a classical Argumentation Framework allows to compute semantics by taking into account the different importance of each argument. We represent a Weighted Argumentation Framework by a non-binary matrix, and we characterize the basic extensions (such as w-admissible, w- stable, w-complete) by analysing sub-blocks of this matrix. Also, we show how to reduce the matrix into another one of smaller size, that is equivalent to the original one for the determination of extensions. Furthermore, we provide two algorithms that allow to build incrementally w-grounded and w-preferred extensions starting from a w-admissible extension.