On Looking for Local Expansion Invariants in Argumentation Semantics: a Preliminary Report
Paper and Code
Jul 30, 2018
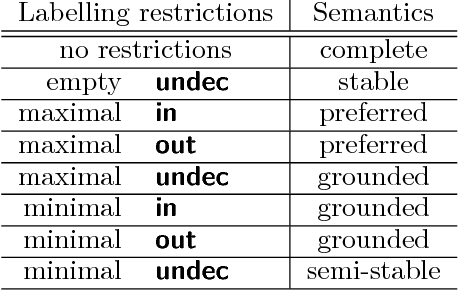
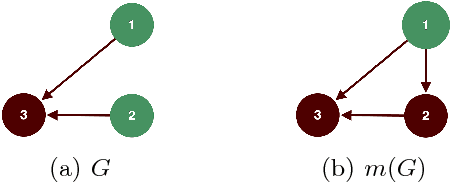
We study invariant local expansion operators for conflict-free and admissible sets in Abstract Argumentation Frameworks (AFs). Such operators are directly applied on AFs, and are invariant with respect to a chosen "semantics" (that is w.r.t. each of the conflict free/admissible set of arguments). Accordingly, we derive a definition of robustness for AFs in terms of the number of times such operators can be applied without producing any change in the chosen semantics.
* Proceedings of the Thirty-First International Florida Artificial
Intelligence Research Society Conference, {FLAIRS} 2018, Melbourne, Florida,
{USA.} May 21-23 2018. Pages 537--540
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge