Hyper Temporal Networks

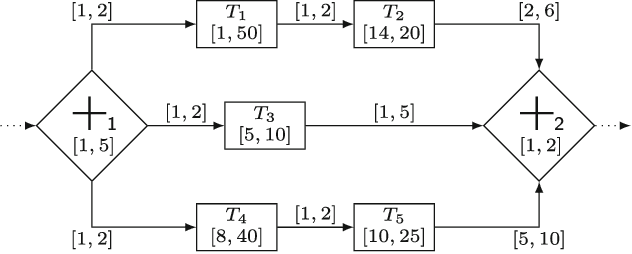
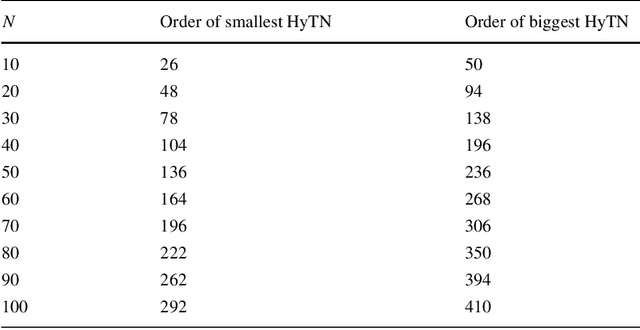
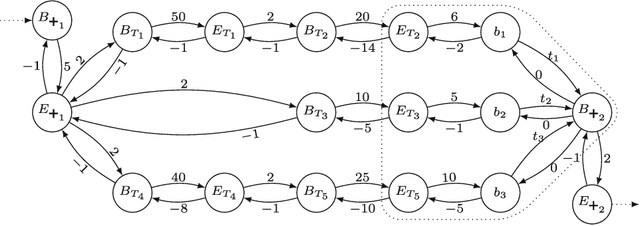
Simple Temporal Networks (STNs) provide a powerful and general tool for representing conjunctions of maximum delay constraints over ordered pairs of temporal variables. In this paper we introduce Hyper Temporal Networks (HyTNs), a strict generalization of STNs, to overcome the limitation of considering only conjunctions of constraints but maintaining a practical efficiency in the consistency check of the instances. In a Hyper Temporal Network a single temporal hyperarc constraint may be defined as a set of two or more maximum delay constraints which is satisfied when at least one of these delay constraints is satisfied. HyTNs are meant as a light generalization of STNs offering an interesting compromise. On one side, there exist practical pseudo-polynomial time algorithms for checking consistency and computing feasible schedules for HyTNs. On the other side, HyTNs offer a more powerful model accommodating natural constraints that cannot be expressed by STNs like Trigger off exactly delta min before (after) the occurrence of the first (last) event in a set., which are used to represent synchronization events in some process aware information systems/workflow models proposed in the literature.

Dynamic Consistency of Conditional Simple Temporal Networks via Mean Payoff Games: a Singly-Exponential Time DC-Checking

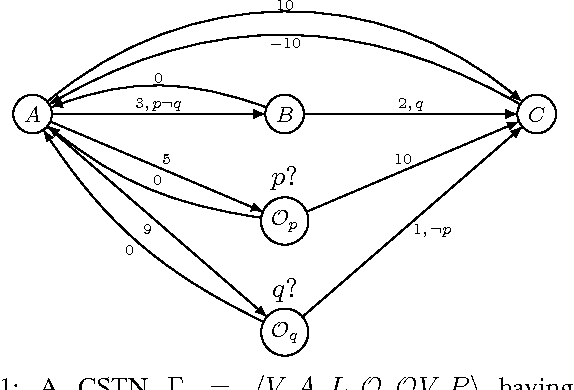
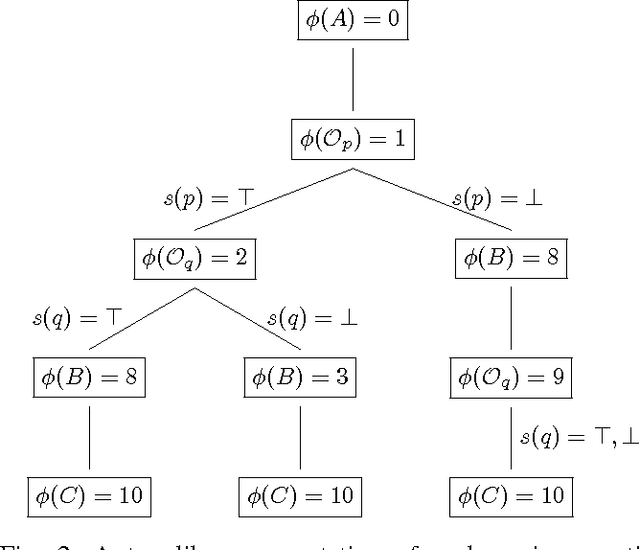
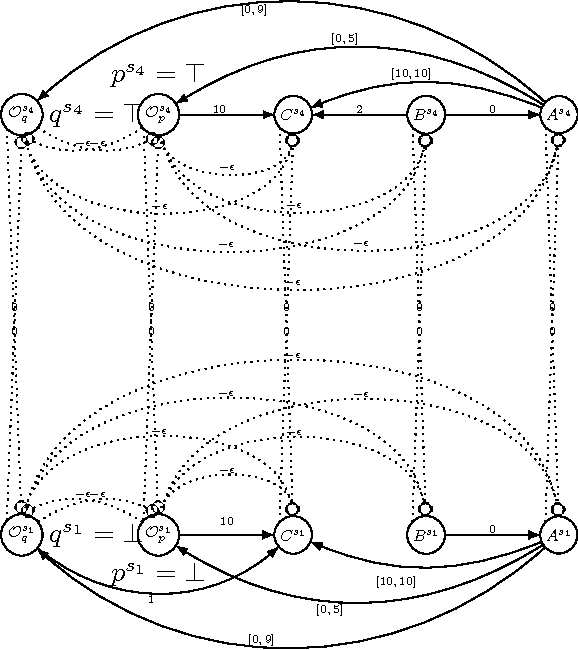
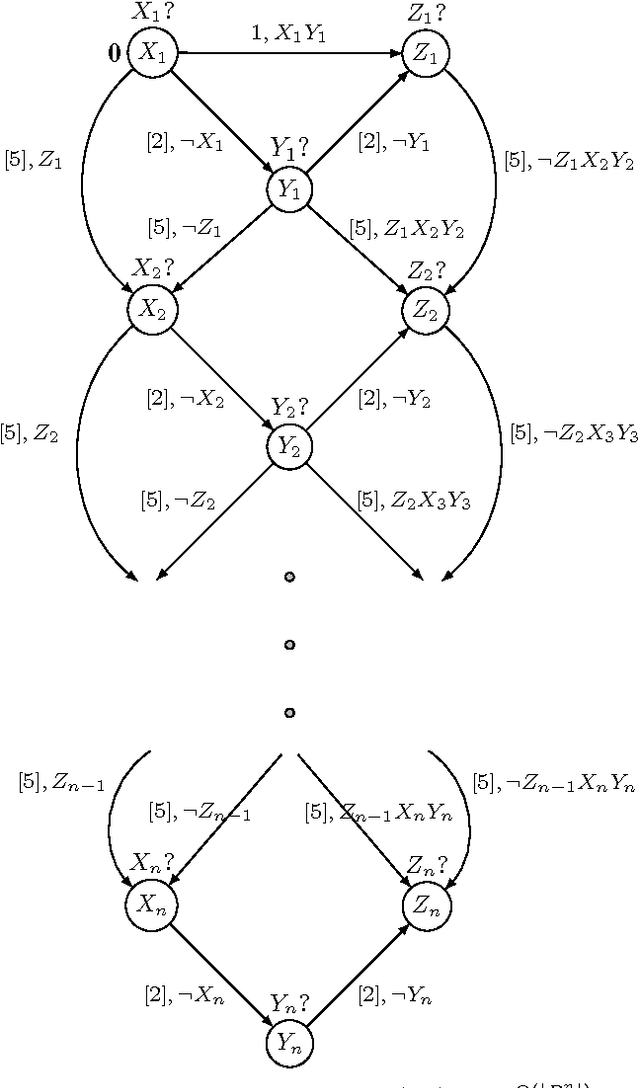
Conditional Simple Temporal Network (CSTN) is a constraint-based graph-formalism for conditional temporal planning. It offers a more flexible formalism than the equivalent CSTP model of Tsamardinos, Vidal and Pollack, from which it was derived mainly as a sound formalization. Three notions of consistency arise for CSTNs and CSTPs: weak, strong, and dynamic. Dynamic consistency is the most interesting notion, but it is also the most challenging and it was conjectured to be hard to assess. Tsamardinos, Vidal and Pollack gave a doubly-exponential time algorithm for deciding whether a CSTN is dynamically-consistent and to produce, in the positive case, a dynamic execution strategy of exponential size. In the present work we offer a proof that deciding whether a CSTN is dynamically-consistent is coNP-hard and provide the first singly-exponential time algorithm for this problem, also producing a dynamic execution strategy whenever the input CSTN is dynamically-consistent. The algorithm is based on a novel connection with Mean Payoff Games, a family of two-player combinatorial games on graphs well known for having applications in model-checking and formal verification. The presentation of such connection is mediated by the Hyper Temporal Network model, a tractable generalization of Simple Temporal Networks whose consistency checking is equivalent to determining Mean Payoff Games. In order to analyze the algorithm we introduce a refined notion of dynamic-consistency, named \epsilon-dynamic-consistency, and present a sharp lower bounding analysis on the critical value of the reaction time \hat{\varepsilon} where the CSTN transits from being, to not being, dynamically-consistent. The proof technique introduced in this analysis of \hat{\varepsilon} is applicable more in general when dealing with linear difference constraints which include strict inequalities.