Dynamic Consistency of Conditional Simple Temporal Networks via Mean Payoff Games: a Singly-Exponential Time DC-Checking
Paper and Code
Jul 17, 2015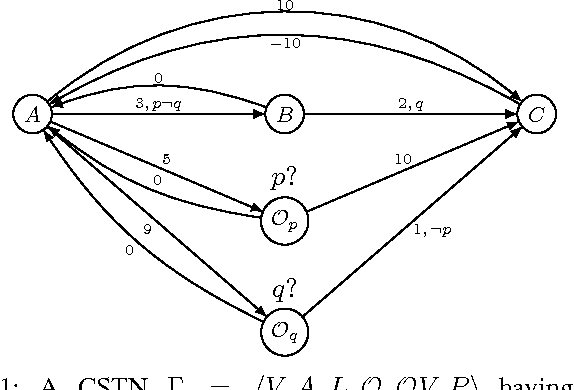
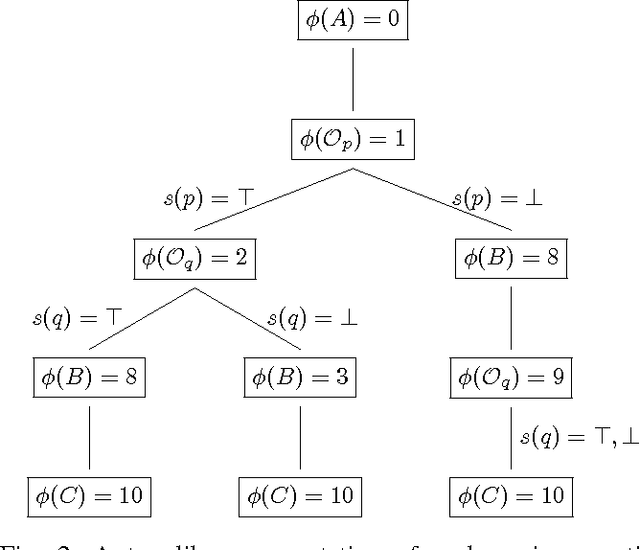
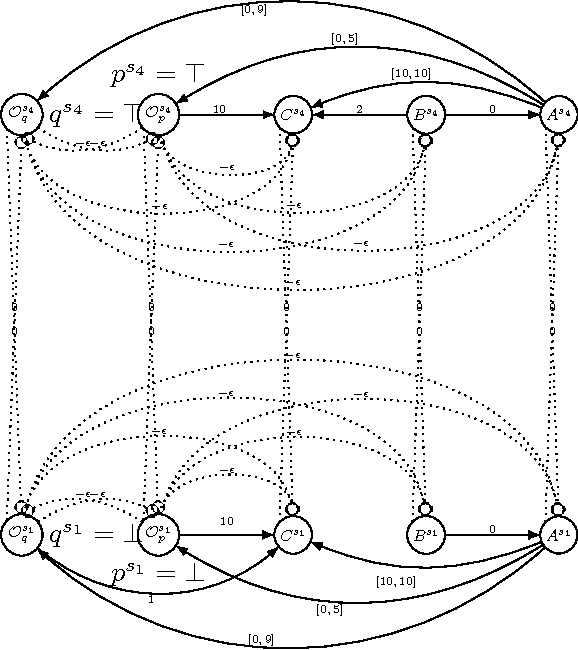
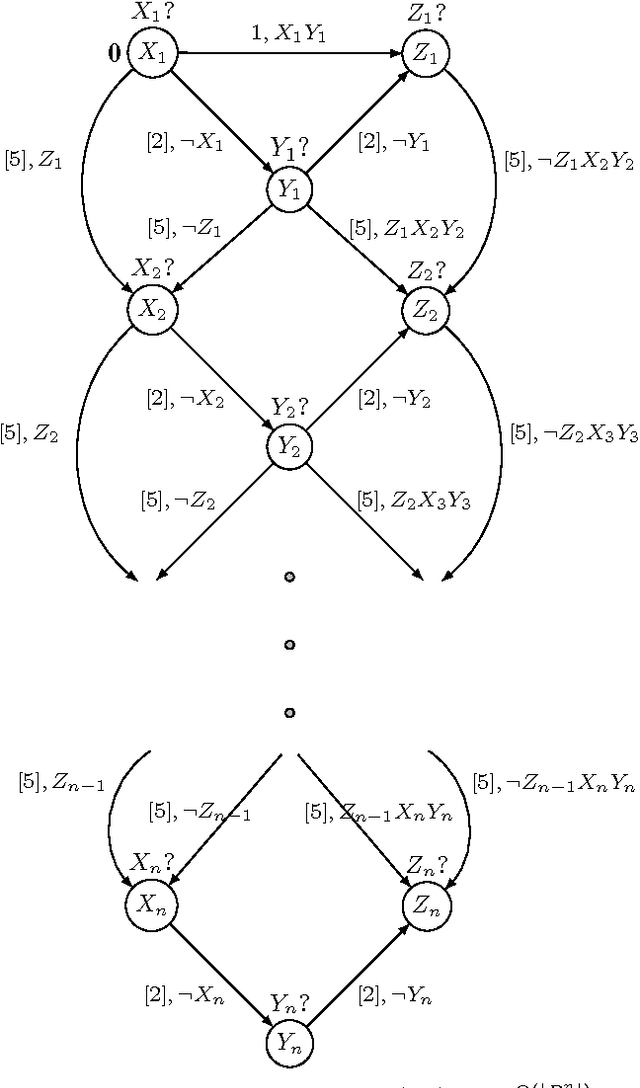
Conditional Simple Temporal Network (CSTN) is a constraint-based graph-formalism for conditional temporal planning. It offers a more flexible formalism than the equivalent CSTP model of Tsamardinos, Vidal and Pollack, from which it was derived mainly as a sound formalization. Three notions of consistency arise for CSTNs and CSTPs: weak, strong, and dynamic. Dynamic consistency is the most interesting notion, but it is also the most challenging and it was conjectured to be hard to assess. Tsamardinos, Vidal and Pollack gave a doubly-exponential time algorithm for deciding whether a CSTN is dynamically-consistent and to produce, in the positive case, a dynamic execution strategy of exponential size. In the present work we offer a proof that deciding whether a CSTN is dynamically-consistent is coNP-hard and provide the first singly-exponential time algorithm for this problem, also producing a dynamic execution strategy whenever the input CSTN is dynamically-consistent. The algorithm is based on a novel connection with Mean Payoff Games, a family of two-player combinatorial games on graphs well known for having applications in model-checking and formal verification. The presentation of such connection is mediated by the Hyper Temporal Network model, a tractable generalization of Simple Temporal Networks whose consistency checking is equivalent to determining Mean Payoff Games. In order to analyze the algorithm we introduce a refined notion of dynamic-consistency, named \epsilon-dynamic-consistency, and present a sharp lower bounding analysis on the critical value of the reaction time \hat{\varepsilon} where the CSTN transits from being, to not being, dynamically-consistent. The proof technique introduced in this analysis of \hat{\varepsilon} is applicable more in general when dealing with linear difference constraints which include strict inequalities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge