FIRE-CIR: Fine-grained Reasoning for Composed Fashion Image Retrieval

Composed image retrieval (CIR) aims to retrieve a target image that depicts a reference image modified by a textual description. While recent vision-language models (VLMs) achieve promising CIR performance by embedding images and text into a shared space for retrieval, they often fail to reason about what to preserve and what to change. This limitation hinders interpretability and yields suboptimal results, particularly in fine-grained domains like fashion. In this paper, we introduce FIRE-CIR, a model that brings compositional reasoning and interpretability to fashion CIR. Instead of relying solely on embedding similarity, FIRE-CIR performs question-driven visual reasoning: it automatically generates attribute-focused visual questions derived from the modification text, and verifies the corresponding visual evidence in both reference and candidate images. To train such a reasoning system, we automatically construct a large-scale fashion-specific visual question answering dataset, containing questions requiring either single- or dual-image analysis. During retrieval, our model leverages this explicit reasoning to re-rank candidate results, filtering out images inconsistent with the intended modifications. Experimental results on the Fashion IQ benchmark show that FIRE-CIR outperforms state-of-the-art methods in retrieval accuracy. It also provides interpretable, attribute-level insights into retrieval decisions.

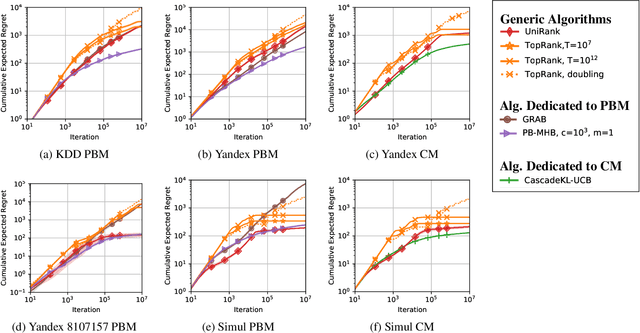
UniRank: Unimodal Bandit Algorithm for Online Ranking

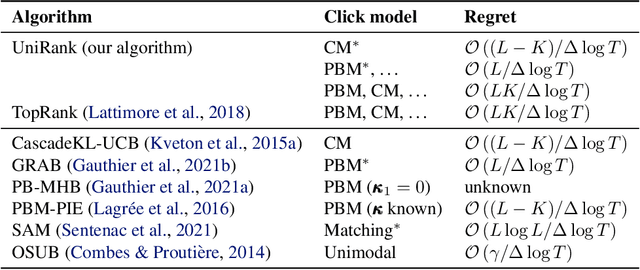
We tackle a new emerging problem, which is finding an optimal monopartite matching in a weighted graph. The semi-bandit version, where a full matching is sampled at each iteration, has been addressed by \cite{ADMA}, creating an algorithm with an expected regret matching $O(\frac{L\log(L)}{\Delta}\log(T))$ with $2L$ players, $T$ iterations and a minimum reward gap $\Delta$. We reduce this bound in two steps. First, as in \cite{GRAB} and \cite{UniRank} we use the unimodality property of the expected reward on the appropriate graph to design an algorithm with a regret in $O(L\frac{1}{\Delta}\log(T))$. Secondly, we show that by moving the focus towards the main question `\emph{Is user $i$ better than user $j$?}' this regret becomes $O(L\frac{\Delta}{\tilde{\Delta}^2}\log(T))$, where $\Tilde{\Delta} > \Delta$ derives from a better way of comparing users. Some experimental results finally show these theoretical results are corroborated in practice.

Position-Based Multiple-Play Bandits with Thompson Sampling

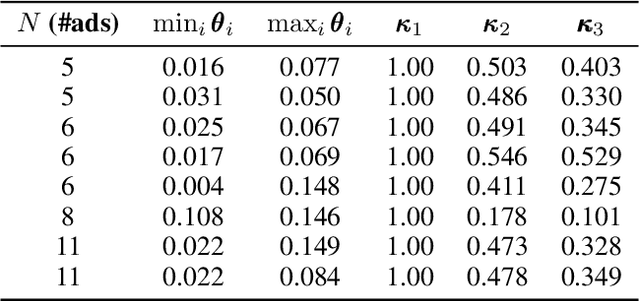
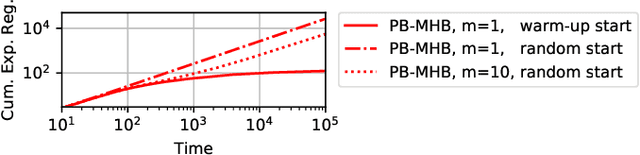
Multiple-play bandits aim at displaying relevant items at relevant positions on a web page. We introduce a new bandit-based algorithm, PB-MHB, for online recommender systems which uses the Thompson sampling framework. This algorithm handles a display setting governed by the position-based model. Our sampling method does not require as input the probability of a user to look at a given position in the web page which is, in practice, very difficult to obtain. Experiments on simulated and real datasets show that our method, with fewer prior information, deliver better recommendations than state-of-the-art algorithms.