A two-head loss function for deep Average-K classification

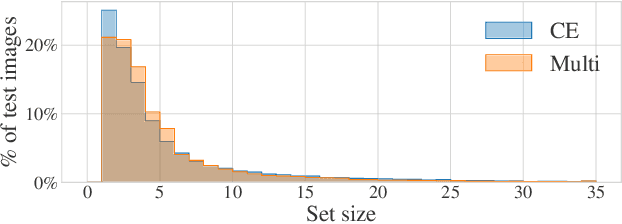
Average-K classification is an alternative to top-K classification in which the number of labels returned varies with the ambiguity of the input image but must average to K over all the samples. A simple method to solve this task is to threshold the softmax output of a model trained with the cross-entropy loss. This approach is theoretically proven to be asymptotically consistent, but it is not guaranteed to be optimal for a finite set of samples. In this paper, we propose a new loss function based on a multi-label classification head in addition to the classical softmax. This second head is trained using pseudo-labels generated by thresholding the softmax head while guaranteeing that K classes are returned on average. We show that this approach allows the model to better capture ambiguities between classes and, as a result, to return more consistent sets of possible classes. Experiments on two datasets from the literature demonstrate that our approach outperforms the softmax baseline, as well as several other loss functions more generally designed for weakly supervised multi-label classification. The gains are larger the higher the uncertainty, especially for classes with few samples.

Stochastic smoothing of the top-K calibrated hinge loss for deep imbalanced classification

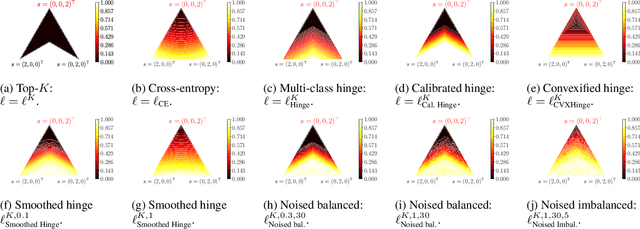
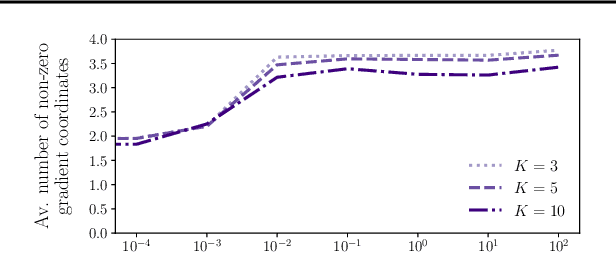
In modern classification tasks, the number of labels is getting larger and larger, as is the size of the datasets encountered in practice. As the number of classes increases, class ambiguity and class imbalance become more and more problematic to achieve high top-1 accuracy. Meanwhile, Top-K metrics (metrics allowing K guesses) have become popular, especially for performance reporting. Yet, proposing top-K losses tailored for deep learning remains a challenge, both theoretically and practically. In this paper we introduce a stochastic top-K hinge loss inspired by recent developments on top-K calibrated losses. Our proposal is based on the smoothing of the top-K operator building on the flexible "perturbed optimizer" framework. We show that our loss function performs very well in the case of balanced datasets, while benefiting from a significantly lower computational time than the state-of-the-art top-K loss function. In addition, we propose a simple variant of our loss for the imbalanced case. Experiments on a heavy-tailed dataset show that our loss function significantly outperforms other baseline loss functions.