The algorithm of noisy k-means

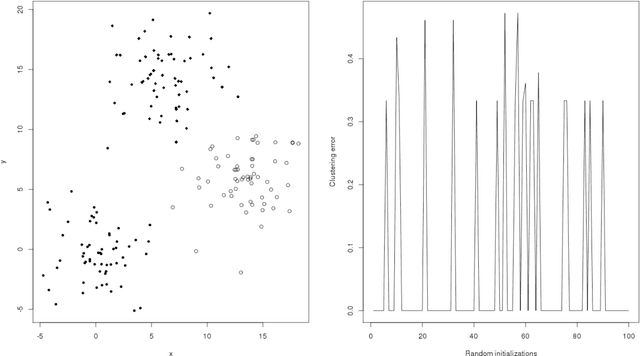
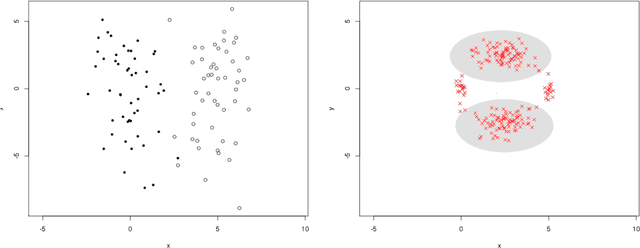
In this note, we introduce a new algorithm to deal with finite dimensional clustering with errors in variables. The design of this algorithm is based on recent theoretical advances (see Loustau (2013a,b)) in statistical learning with errors in variables. As the previous mentioned papers, the algorithm mixes different tools from the inverse problem literature and the machine learning community. Coarsely, it is based on a two-step procedure: (1) a deconvolution step to deal with noisy inputs and (2) Newton's iterations as the popular k-means.

Simultaneous model-based clustering and visualization in the Fisher discriminative subspace

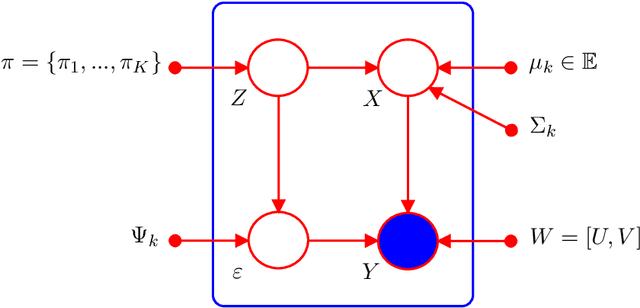
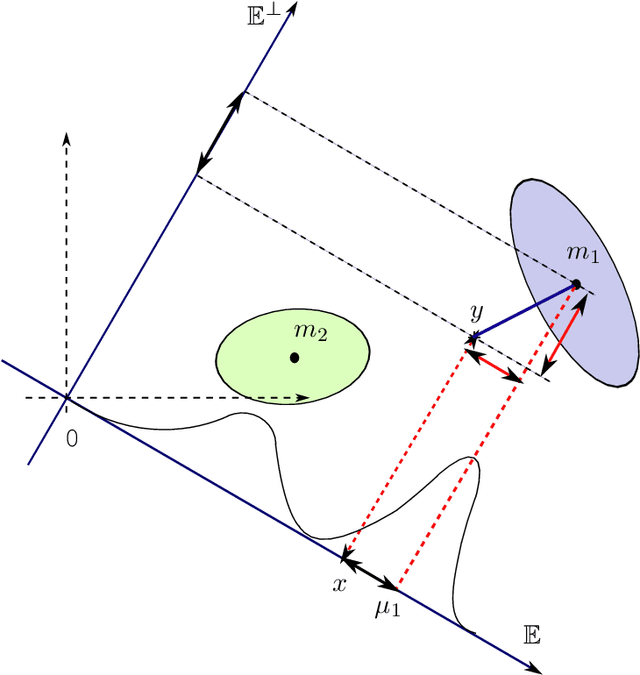
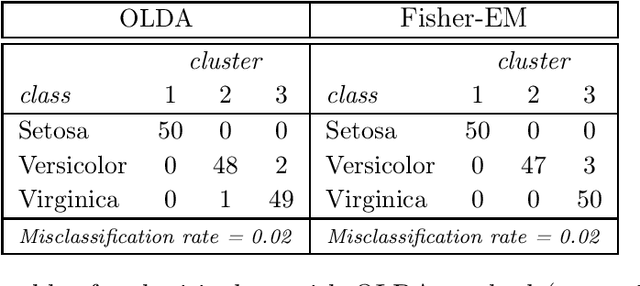
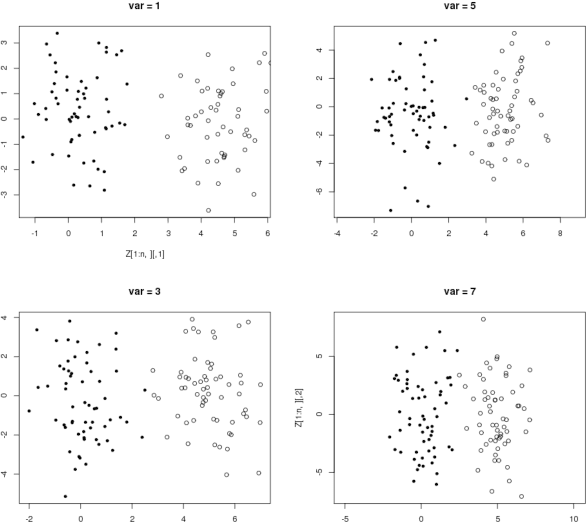
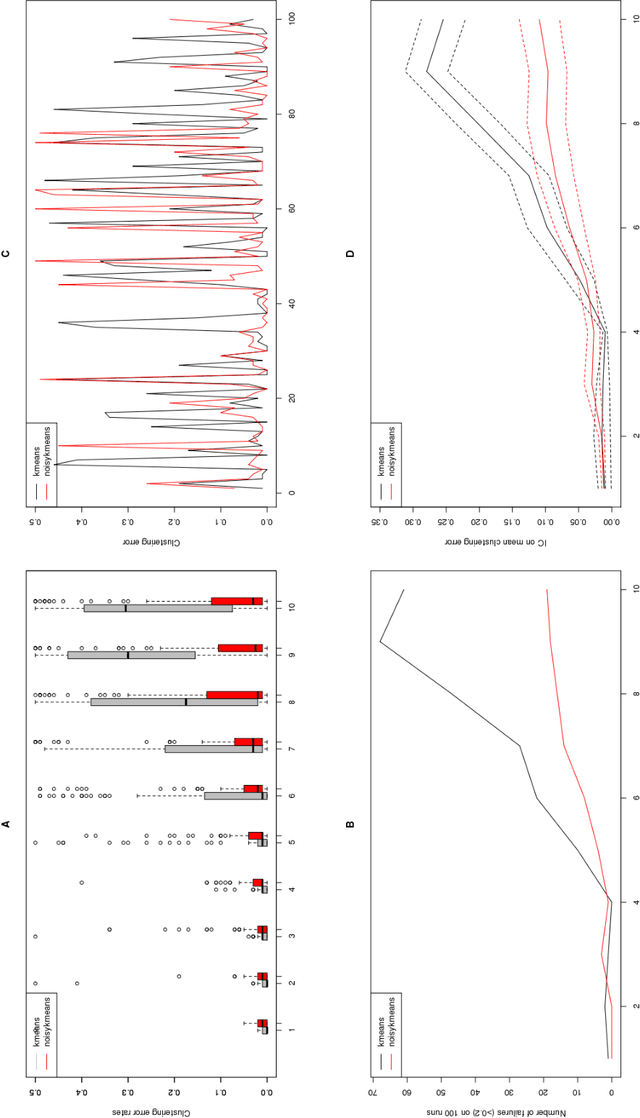
Clustering in high-dimensional spaces is nowadays a recurrent problem in many scientific domains but remains a difficult task from both the clustering accuracy and the result understanding points of view. This paper presents a discriminative latent mixture (DLM) model which fits the data in a latent orthonormal discriminative subspace with an intrinsic dimension lower than the dimension of the original space. By constraining model parameters within and between groups, a family of 12 parsimonious DLM models is exhibited which allows to fit onto various situations. An estimation algorithm, called the Fisher-EM algorithm, is also proposed for estimating both the mixture parameters and the discriminative subspace. Experiments on simulated and real datasets show that the proposed approach performs better than existing clustering methods while providing a useful representation of the clustered data. The method is as well applied to the clustering of mass spectrometry data.