Cahngyong Niu
Sparse Group Restricted Boltzmann Machines
Aug 30, 2010
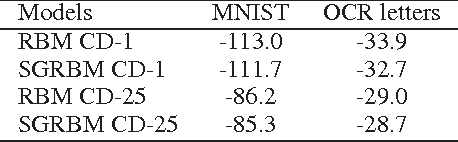


Abstract:Since learning is typically very slow in Boltzmann machines, there is a need to restrict connections within hidden layers. However, the resulting states of hidden units exhibit statistical dependencies. Based on this observation, we propose using $l_1/l_2$ regularization upon the activation possibilities of hidden units in restricted Boltzmann machines to capture the loacal dependencies among hidden units. This regularization not only encourages hidden units of many groups to be inactive given observed data but also makes hidden units within a group compete with each other for modeling observed data. Thus, the $l_1/l_2$ regularization on RBMs yields sparsity at both the group and the hidden unit levels. We call RBMs trained with the regularizer \emph{sparse group} RBMs. The proposed sparse group RBMs are applied to three tasks: modeling patches of natural images, modeling handwritten digits and pretaining a deep networks for a classification task. Furthermore, we illustrate the regularizer can also be applied to deep Boltzmann machines, which lead to sparse group deep Boltzmann machines. When adapted to the MNIST data set, a two-layer sparse group Boltzmann machine achieves an error rate of $0.84\%$, which is, to our knowledge, the best published result on the permutation-invariant version of the MNIST task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge