Quickest Detection over Sensor Networks with Unknown Post-Change Distribution

We propose a quickest change detection problem over sensor networks where both the subset of sensors undergoing a change and the local post-change distributions are unknown. Each sensor in the network observes a local discrete time random process over a finite alphabet. Initially, the observations are independent and identically distributed (i.i.d.) with known pre-change distributions independent from other sensors. At a fixed but unknown change point, a fixed but unknown subset of the sensors undergo a change and start observing samples from an unknown distribution. We assume the change can be quantified using concave (or convex) local statistics over the space of distributions. We propose an asymptotically optimal and computationally tractable stopping time for Lorden's criterion. Under this scenario, our proposed method uses a concave global cumulative sum (CUSUM) statistic at the fusion center and suppresses the most likely false alarms using information projection. Finally, we show some numerical results of the simulation of our algorithm for the problem described.

Source Coding Based mmWave Channel Estimation with Deep Learning Based Decoding

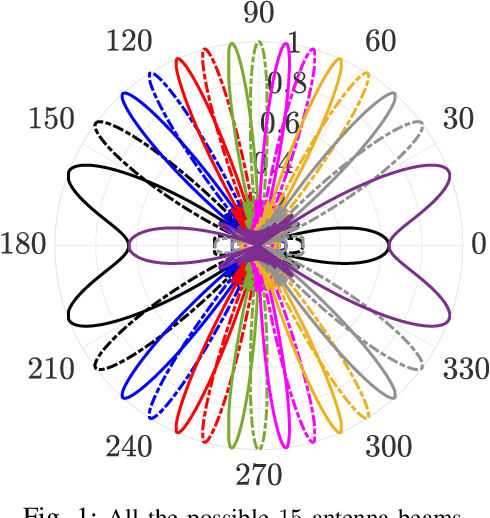
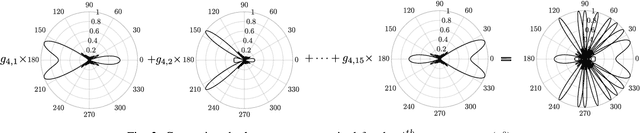
mmWave technology is set to become a main feature of next generation wireless networks, e.g., 5G mobile and WiFi 802.11ad/ay. Among the basic and most fundamental challenges facing mmWave is the ability to overcome its unfavorable propagation characteristics using energy efficient solutions. This has been addressed using innovative transceiver architectures. However, these architectures have their own limitations when it comes to channel estimation. This paper focuses on channel estimation and poses it as a source compression problem, where channel measurements are designed to mimic an encoded (compressed) version of the channel. We show that linear source codes can significantly reduce the number of channel measurements required to discover all channel paths. We also propose a deep-learning-based approach for decoding the obtained measurements, which enables high-speed and efficient channel discovery.