Quickest Detection over Sensor Networks with Unknown Post-Change Distribution
Paper and Code
Dec 23, 2020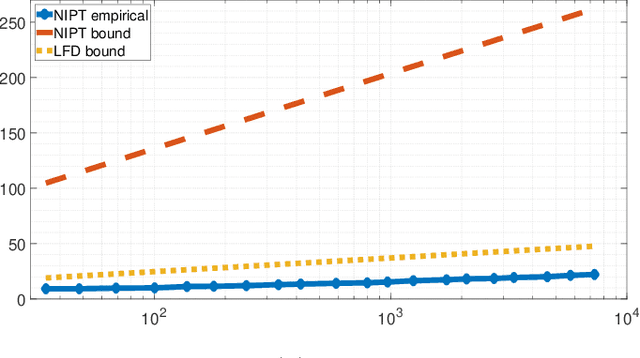
We propose a quickest change detection problem over sensor networks where both the subset of sensors undergoing a change and the local post-change distributions are unknown. Each sensor in the network observes a local discrete time random process over a finite alphabet. Initially, the observations are independent and identically distributed (i.i.d.) with known pre-change distributions independent from other sensors. At a fixed but unknown change point, a fixed but unknown subset of the sensors undergo a change and start observing samples from an unknown distribution. We assume the change can be quantified using concave (or convex) local statistics over the space of distributions. We propose an asymptotically optimal and computationally tractable stopping time for Lorden's criterion. Under this scenario, our proposed method uses a concave global cumulative sum (CUSUM) statistic at the fusion center and suppresses the most likely false alarms using information projection. Finally, we show some numerical results of the simulation of our algorithm for the problem described.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge