Global optimization of Lipschitz functions

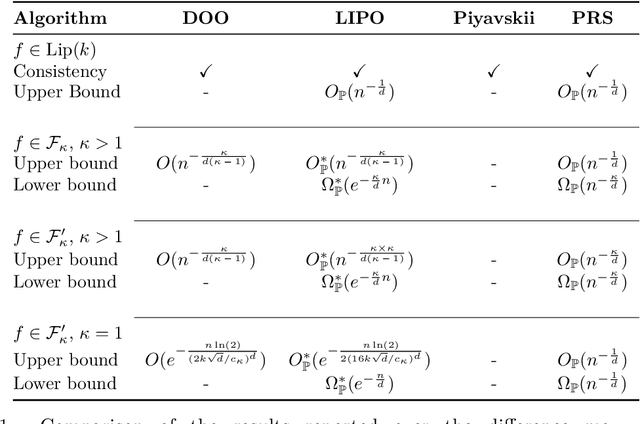
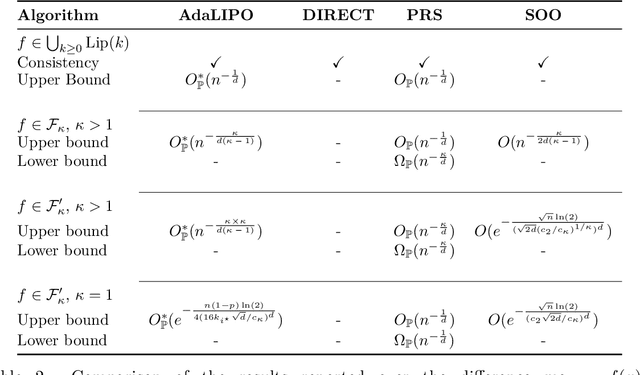
The goal of the paper is to design sequential strategies which lead to efficient optimization of an unknown function under the only assumption that it has a finite Lipschitz constant. We first identify sufficient conditions for the consistency of generic sequential algorithms and formulate the expected minimax rate for their performance. We introduce and analyze a first algorithm called LIPO which assumes the Lipschitz constant to be known. Consistency, minimax rates for LIPO are proved, as well as fast rates under an additional H\"older like condition. An adaptive version of LIPO is also introduced for the more realistic setup where the Lipschitz constant is unknown and has to be estimated along with the optimization. Similar theoretical guarantees are shown to hold for the adaptive LIPO algorithm and a numerical assessment is provided at the end of the paper to illustrate the potential of this strategy with respect to state-of-the-art methods over typical benchmark problems for global optimization.

A ranking approach to global optimization

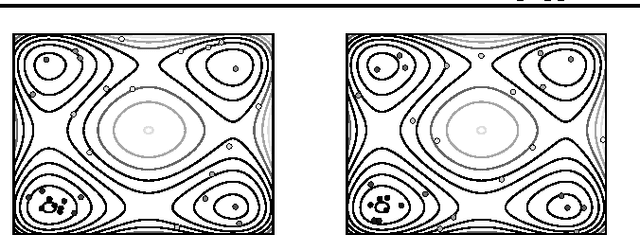
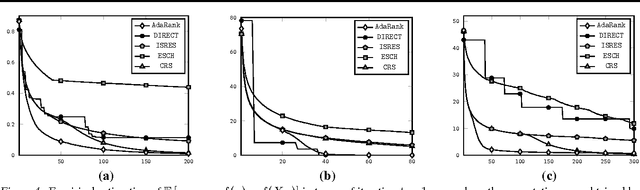
We consider the problem of maximizing an unknown function over a compact and convex set using as few observations as possible. We observe that the optimization of the function essentially relies on learning the induced bipartite ranking rule of f. Based on this idea, we relate global optimization to bipartite ranking which allows to address problems with high dimensional input space, as well as cases of functions with weak regularity properties. The paper introduces novel meta-algorithms for global optimization which rely on the choice of any bipartite ranking method. Theoretical properties are provided as well as convergence guarantees and equivalences between various optimization methods are obtained as a by-product. Eventually, numerical evidence is given to show that the main algorithm of the paper which adapts empirically to the underlying ranking structure essentially outperforms existing state-of-the-art global optimization algorithms in typical benchmarks.

Optimization for Gaussian Processes via Chaining

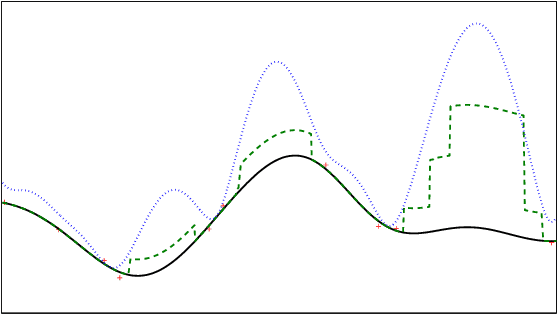
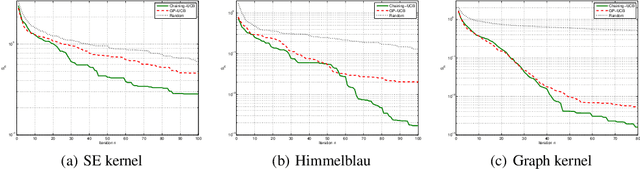
In this paper, we consider the problem of stochastic optimization under a bandit feedback model. We generalize the GP-UCB algorithm [Srinivas and al., 2012] to arbitrary kernels and search spaces. To do so, we use a notion of localized chaining to control the supremum of a Gaussian process, and provide a novel optimization scheme based on the computation of covering numbers. The theoretical bounds we obtain on the cumulative regret are more generic and present the same convergence rates as the GP-UCB algorithm. Finally, the algorithm is shown to be empirically more efficient than its natural competitors on simple and complex input spaces.