Optimization for Gaussian Processes via Chaining

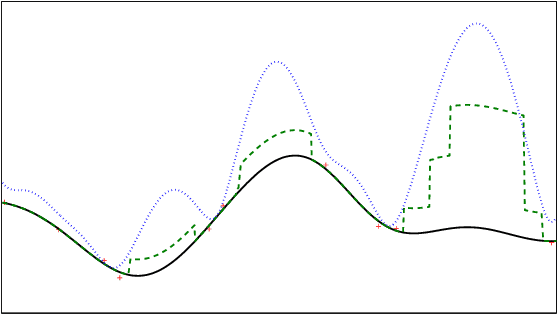
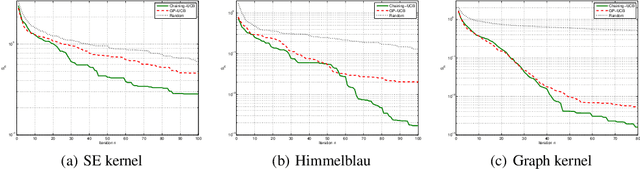
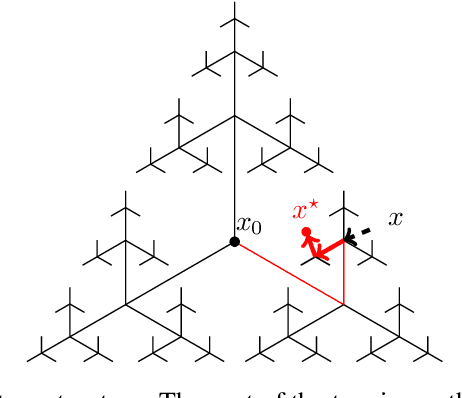
In this paper, we consider the problem of stochastic optimization under a bandit feedback model. We generalize the GP-UCB algorithm [Srinivas and al., 2012] to arbitrary kernels and search spaces. To do so, we use a notion of localized chaining to control the supremum of a Gaussian process, and provide a novel optimization scheme based on the computation of covering numbers. The theoretical bounds we obtain on the cumulative regret are more generic and present the same convergence rates as the GP-UCB algorithm. Finally, the algorithm is shown to be empirically more efficient than its natural competitors on simple and complex input spaces.