Error Optimization: Overcoming Exponential Signal Decay in Deep Predictive Coding Networks

Predictive Coding (PC) offers a biologically plausible alternative to backpropagation for neural network training, yet struggles with deeper architectures. This paper identifies the root cause: an inherent signal decay problem where gradients attenuate exponentially with depth, becoming computationally negligible due to numerical precision constraints. To address this fundamental limitation, we introduce Error Optimization (EO), a novel reparameterization that preserves PC's theoretical properties while eliminating signal decay. By optimizing over prediction errors rather than states, EO enables signals to reach all layers simultaneously and without attenuation, converging orders of magnitude faster than standard PC. Experiments across multiple architectures and datasets demonstrate that EO matches backpropagation's performance even for deeper models where conventional PC struggles. Besides practical improvements, our work provides theoretical insight into PC dynamics and establishes a foundation for scaling biologically-inspired learning to deeper architectures on digital hardware and beyond.

Exploring the Temperature-Dependent Phase Transition in Modern Hopfield Networks

The recent discovery of a connection between Transformers and Modern Hopfield Networks (MHNs) has reignited the study of neural networks from a physical energy-based perspective. This paper focuses on the pivotal effect of the inverse temperature hyperparameter $\beta$ on the distribution of energy minima of the MHN. To achieve this, the distribution of energy minima is tracked in a simplified MHN in which equidistant normalised patterns are stored. This network demonstrates a phase transition at a critical temperature $\beta_{\text{c}}$, from a single global attractor towards highly pattern specific minima as $\beta$ is increased. Importantly, the dynamics are not solely governed by the hyperparameter $\beta$ but are instead determined by an effective inverse temperature $\beta_{\text{eff}}$ which also depends on the distribution and size of the stored patterns. Recognizing the role of hyperparameters in the MHN could, in the future, aid researchers in the domain of Transformers to optimise their initial choices, potentially reducing the necessity for time and energy expensive hyperparameter fine-tuning.

Accelerating Hierarchical Associative Memory: A Deep Equilibrium Approach

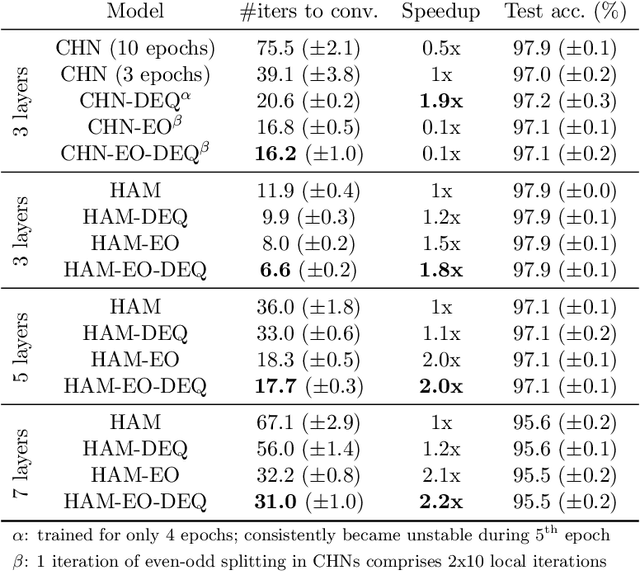
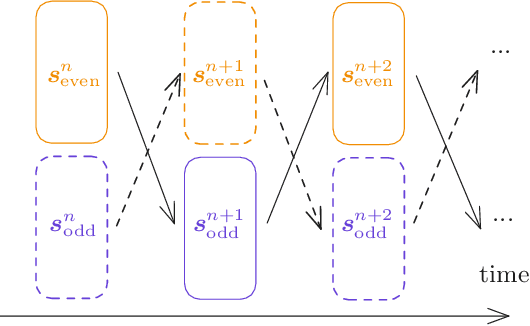
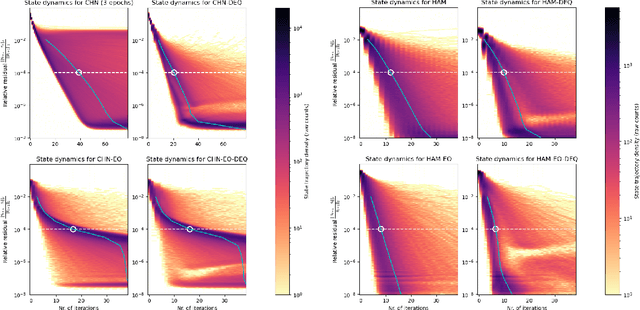
Hierarchical Associative Memory models have recently been proposed as a versatile extension of continuous Hopfield networks. In order to facilitate future research on such models, especially at scale, we focus on increasing their simulation efficiency on digital hardware. In particular, we propose two strategies to speed up memory retrieval in these models, which corresponds to their use at inference, but is equally important during training. First, we show how they can be cast as Deep Equilibrium Models, which allows using faster and more stable solvers. Second, inspired by earlier work, we show that alternating optimization of the even and odd layers accelerates memory retrieval by a factor close to two. Combined, these two techniques allow for a much faster energy minimization, as shown in our proof-of-concept experimental results. The code is available at https://github.com/cgoemaere/hamdeq