Accelerated and interpretable oblique random survival forests

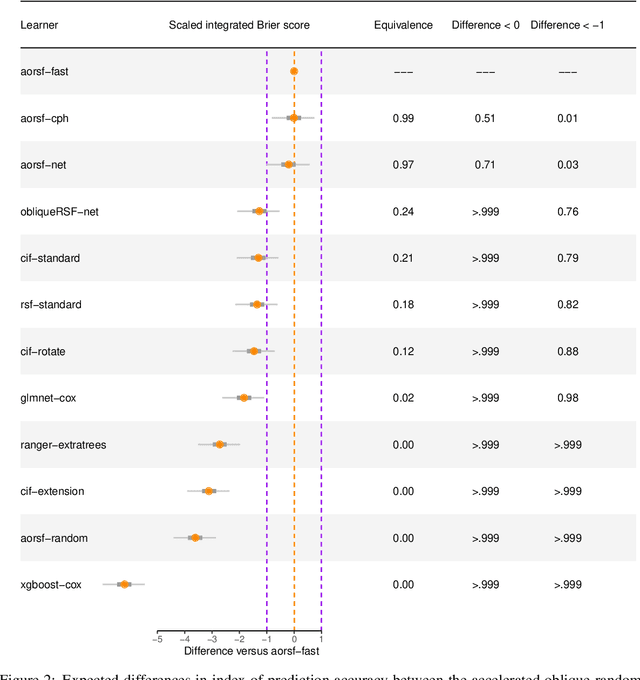
The oblique random survival forest (RSF) is an ensemble supervised learning method for right-censored outcomes. Trees in the oblique RSF are grown using linear combinations of predictors to create branches, whereas in the standard RSF, a single predictor is used. Oblique RSF ensembles often have higher prediction accuracy than standard RSF ensembles. However, assessing all possible linear combinations of predictors induces significant computational overhead that limits applications to large-scale data sets. In addition, few methods have been developed for interpretation of oblique RSF ensembles, and they remain more difficult to interpret compared to their axis-based counterparts. We introduce a method to increase computational efficiency of the oblique RSF and a method to estimate importance of individual predictor variables with the oblique RSF. Our strategy to reduce computational overhead makes use of Newton-Raphson scoring, a classical optimization technique that we apply to the Cox partial likelihood function within each non-leaf node of decision trees. We estimate the importance of individual predictors for the oblique RSF by negating each coefficient used for the given predictor in linear combinations, and then computing the reduction in out-of-bag accuracy. In general benchmarking experiments, we find that our implementation of the oblique RSF is approximately 450 times faster with equivalent discrimination and superior Brier score compared to existing software for oblique RSFs. We find in simulation studies that 'negation importance' discriminates between relevant and irrelevant predictors more reliably than permutation importance, Shapley additive explanations, and a previously introduced technique to measure variable importance with oblique RSFs based on analysis of variance. Methods introduced in the current study are available in the aorsf R package.

Spike-and-Slab Generalized Additive Models and Scalable Algorithms for High-Dimensional Data

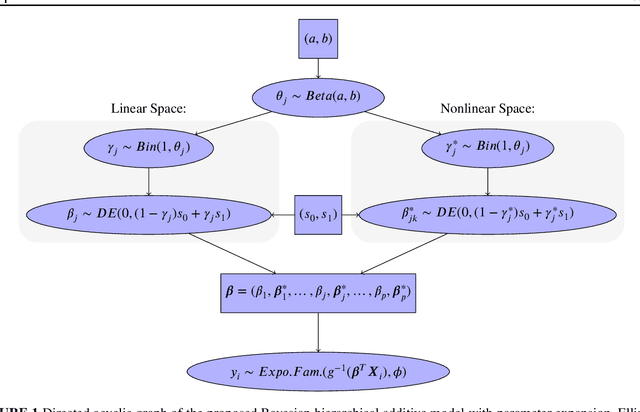
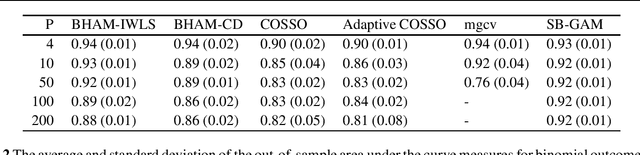
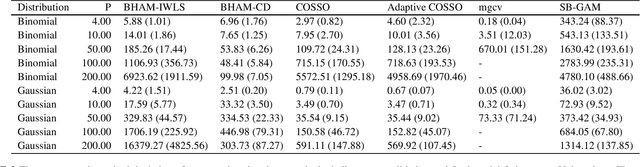
There are proposals that extend the classical generalized additive models (GAMs) to accommodate high-dimensional data ($p>>n$) using group sparse regularization. However, the sparse regularization may induce excess shrinkage when estimating smoothing functions, damaging predictive performance. Moreover, most of these GAMs consider an "all-in-all-out" approach for functional selection, rendering them difficult to answer if nonlinear effects are necessary. While some Bayesian models can address these shortcomings, using Markov chain Monte Carlo algorithms for model fitting creates a new challenge, scalability. Hence, we propose Bayesian hierarchical generalized additive models as a solution: we consider the smoothing penalty for proper shrinkage of curve interpolation and separation of smoothing function linear and nonlinear spaces. A novel spike-and-slab spline prior is proposed to select components of smoothing functions. Two scalable and deterministic algorithms, EM-Coordinate Descent and EM-Iterative Weighted Least Squares, are developed for different utilities. Simulation studies and metabolomics data analyses demonstrate improved predictive or computational performance against state-of-the-art models, mgcv, COSSO and sparse Bayesian GAM. The software implementation of the proposed models is freely available via an R package BHAM.

When to Impute? Imputation before and during cross-validation

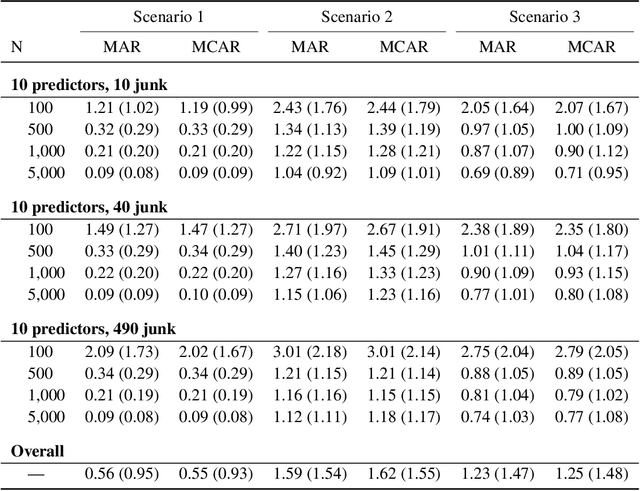
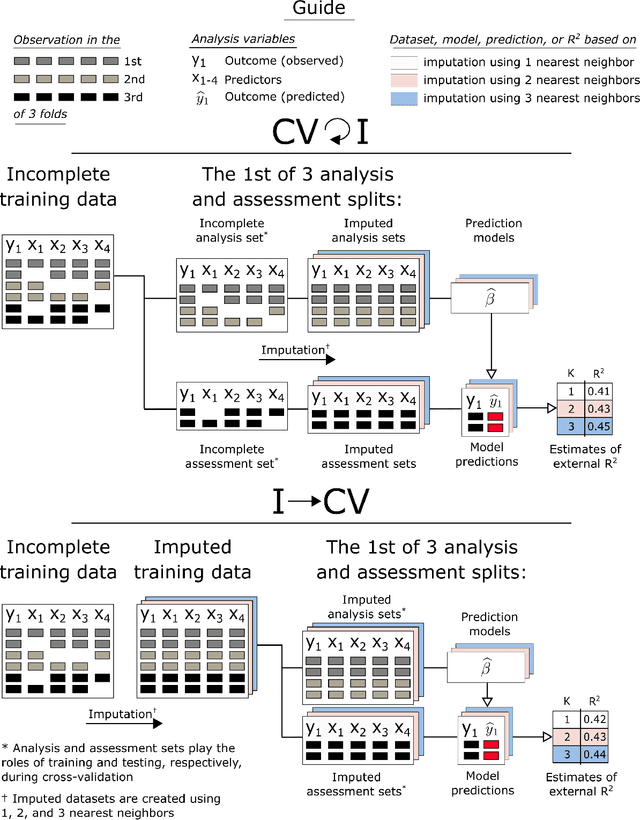
Cross-validation (CV) is a technique used to estimate generalization error for prediction models. For pipeline modeling algorithms (i.e. modeling procedures with multiple steps), it has been recommended the entire sequence of steps be carried out during each replicate of CV to mimic the application of the entire pipeline to an external testing set. While theoretically sound, following this recommendation can lead to high computational costs when a pipeline modeling algorithm includes computationally expensive operations, e.g. imputation of missing values. There is a general belief that unsupervised variable selection (i.e. ignoring the outcome) can be applied before conducting CV without incurring bias, but there is less consensus for unsupervised imputation of missing values. We empirically assessed whether conducting unsupervised imputation prior to CV would result in biased estimates of generalization error or result in poorly selected tuning parameters and thus degrade the external performance of downstream models. Results show that despite optimistic bias, the reduced variance of imputation before CV compared to imputation during each replicate of CV leads to a lower overall root mean squared error for estimation of the true external R-squared and the performance of models tuned using CV with imputation before versus during each replication is minimally different. In conclusion, unsupervised imputation before CV appears valid in certain settings and may be a helpful strategy that enables analysts to use more flexible imputation techniques without incurring high computational costs.