Relating Superconducting Optoelectronic Networks to Classical Neurodynamics

The circuits comprising superconducting optoelectronic synapses, dendrites, and neurons are described by numerically cumbersome and formally opaque coupled differential equations. Reference 1 showed that a phenomenological model of superconducting loop neurons eliminates the need to solve the Josephson circuit equations that describe synapses and dendrites. The initial goal of the model was to decrease the time required for simulations, yet an additional benefit of the model was increased transparency of the underlying neural circuit operations and conceptual clarity regarding the connection of loop neurons to other physical systems. Whereas the original model simplified the treatment of the Josephson-junction dynamics, essentially by only considering low-pass versions of the dendritic outputs, the model resorted to an awkward treatment of spikes generated by semiconductor transmitter circuits that required explicitly checking for threshold crossings and distinct treatment of time steps wherein somatic threshold is reached. Here we extend that model to simplify the treatment of spikes coming from somas, again making use of the fact that in neural systems the downstream recipients of spike events almost always perform low-pass filtering. We provide comparisons between the first and second phenomenological models, quantifying the accuracy of the additional approximations. We identify regions of circuit parameter space in which the extended model works well and regions where it works poorly. For some circuit parameters it is possible to represent the downstream dendritic response to a single spike as well as coincidences or sequences of spikes, indicating the model is not simply a reduction to rate coding. The governing equations are shown to be nearly identical to those ubiquitous in the neuroscience literature for modeling leaky-integrator dendrites and neurons.

Programmable Superconducting Optoelectronic Single-Photon Synapses with Integrated Multi-State Memory

The co-location of memory and processing is a core principle of neuromorphic computing. A local memory device for synaptic weight storage has long been recognized as an enabling element for large-scale, high-performance neuromorphic hardware. In this work, we demonstrate programmable superconducting synapses with integrated memories for use in superconducting optoelectronic neural systems. Superconducting nanowire single-photon detectors and Josephson junctions are combined into programmable synaptic circuits that exhibit single-photon sensitivity, memory cells with more than 400 internal states, leaky integration of input spike events, and 0.4 fJ programming energies (including cooling power). These results are attractive for implementing a variety of supervised and unsupervised learning algorithms and lay the foundation for a new hardware platform optimized for large-scale spiking network accelerators.

Phenomenological Model of Superconducting Optoelectronic Loop Neurons

Superconducting optoelectronic loop neurons are a class of circuits potentially conducive to networks for large-scale artificial cognition. These circuits employ superconducting components including single-photon detectors, Josephson junctions, and transformers to achieve neuromorphic functions. To date, all simulations of loop neurons have used first-principles circuit analysis to model the behavior of synapses, dendrites, and neurons. These circuit models are computationally inefficient and leave opaque the relationship between loop neurons and other complex systems. Here we introduce a modeling framework that captures the behavior of the relevant synaptic, dendritic, and neuronal circuits at a phenomenological level without resorting to full circuit equations. Within this compact model, each dendrite is discovered to obey a single nonlinear leaky-integrator ordinary differential equation, while a neuron is modeled as a dendrite with a thresholding element and an additional feedback mechanism for establishing a refractory period. A synapse is modeled as a single-photon detector coupled to a dendrite, where the response of the single-photon detector follows a closed-form expression. We quantify the accuracy of the phenomenological model relative to circuit simulations and find that the approach reduces computational time by a factor of ten thousand while maintaining accuracy of one part in ten thousand. We demonstrate the use of the model with several basic examples. The net increase in computational efficiency enables future simulation of large networks, while the formulation provides a connection to a large body of work in applied mathematics, computational neuroscience, and physical systems such as spin glasses.

Demonstration of Superconducting Optoelectronic Single-Photon Synapses

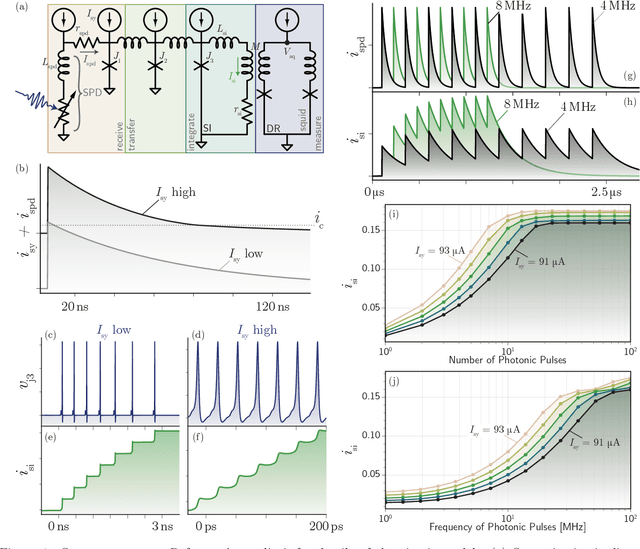
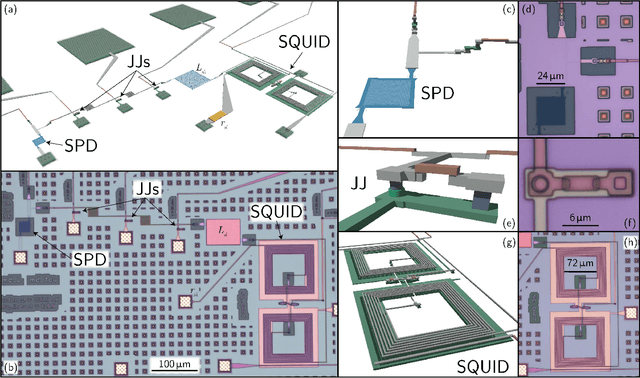
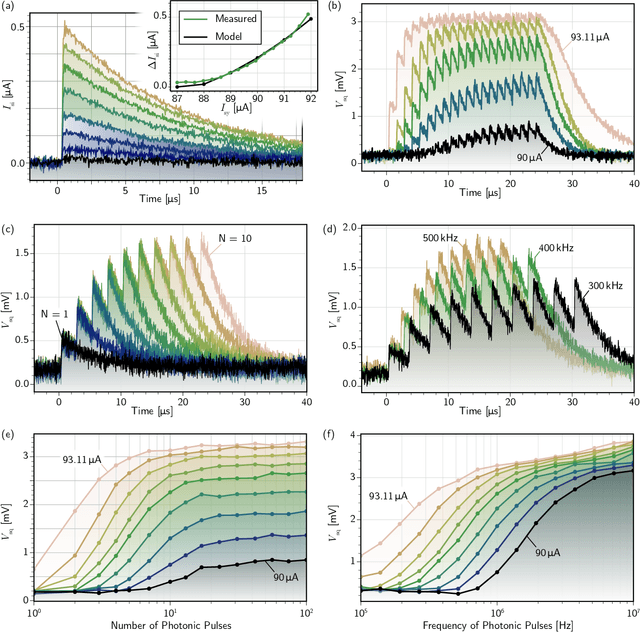
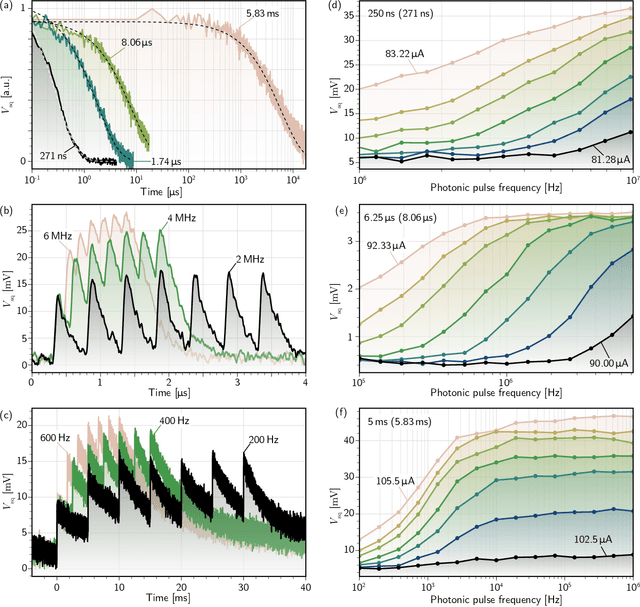
Superconducting optoelectronic hardware is being explored as a path towards artificial spiking neural networks with unprecedented scales of complexity and computational ability. Such hardware combines integrated-photonic components for few-photon, light-speed communication with superconducting circuits for fast, energy-efficient computation. Monolithic integration of superconducting and photonic devices is necessary for the scaling of this technology. In the present work, superconducting-nanowire single-photon detectors are monolithically integrated with Josephson junctions for the first time, enabling the realization of superconducting optoelectronic synapses. We present circuits that perform analog weighting and temporal leaky integration of single-photon presynaptic signals. Synaptic weighting is implemented in the electronic domain so that binary, single-photon communication can be maintained. Records of recent synaptic activity are locally stored as current in superconducting loops. Dendritic and neuronal nonlinearities are implemented with a second stage of Josephson circuitry. The hardware presents great design flexibility, with demonstrated synaptic time constants spanning four orders of magnitude (hundreds of nanoseconds to milliseconds). The synapses are responsive to presynaptic spike rates exceeding 10 MHz and consume approximately 33 aJ of dynamic power per synapse event before accounting for cooling. In addition to neuromorphic hardware, these circuits introduce new avenues towards realizing large-scale single-photon-detector arrays for diverse imaging, sensing, and quantum communication applications.

An active dendritic tree can mitigate fan-in limitations in superconducting neurons

Superconducting electronic circuits have much to offer with regard to neuromorphic hardware. Superconducting quantum interference devices (SQUIDs) can serve as an active element to perform the thresholding operation of a neuron's soma. However, a SQUID has a response function that is periodic in the applied signal. We show theoretically that if one restricts the total input to a SQUID to maintain a monotonically increasing response, a large fraction of synapses must be active to drive a neuron to threshold. We then demonstrate that an active dendritic tree (also based on SQUIDs) can significantly reduce the fraction of synapses that must be active to drive the neuron to threshold. In this context, the inclusion of a dendritic tree provides the dual benefits of enhancing the computational abilities of each neuron and allowing the neuron to spike with sparse input activity.