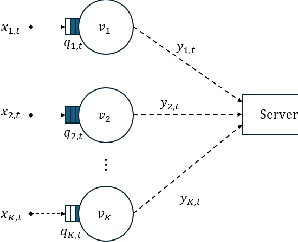
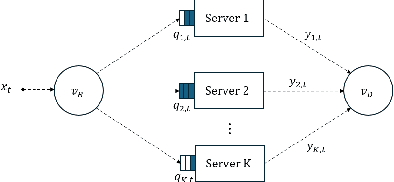
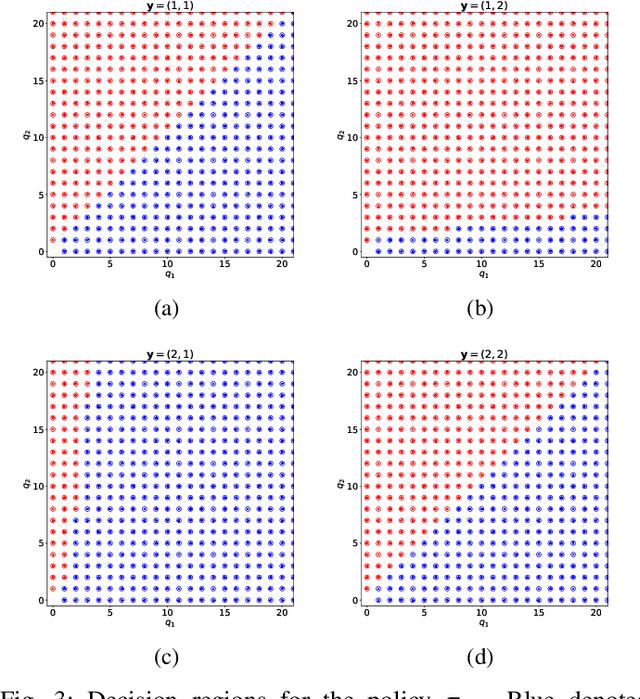
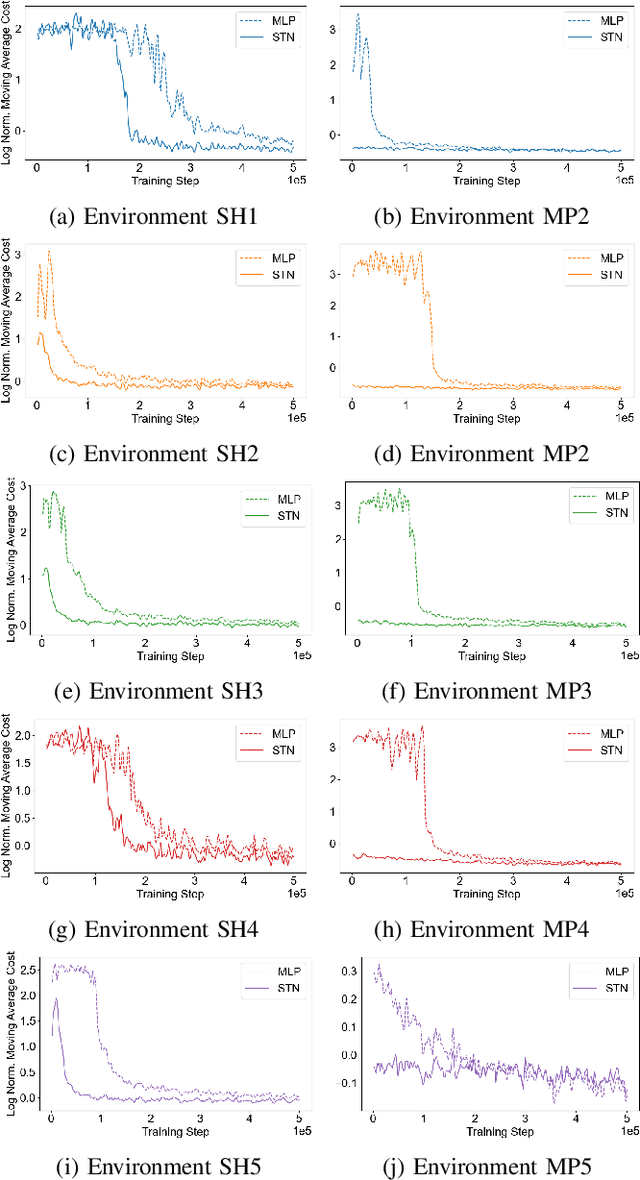
A Novel Switch-Type Policy Network for Resource Allocation Problems: Technical Report

Deep Reinforcement Learning (DRL) has become a powerful tool for developing control policies in queueing networks, but the common use of Multi-layer Perceptron (MLP) neural networks in these applications has significant drawbacks. MLP architectures, while versatile, often suffer from poor sample efficiency and a tendency to overfit training environments, leading to suboptimal performance on new, unseen networks. In response to these issues, we introduce a switch-type neural network (STN) architecture designed to improve the efficiency and generalization of DRL policies in queueing networks. The STN leverages structural patterns from traditional non-learning policies, ensuring consistent action choices across similar states. This design not only streamlines the learning process but also fosters better generalization by reducing the tendency to overfit. Our works presents three key contributions: first, the development of the STN as a more effective alternative to MLPs; second, empirical evidence showing that STNs achieve superior sample efficiency in various training scenarios; and third, experimental results demonstrating that STNs match MLP performance in familiar environments and significantly outperform them in new settings. By embedding domain-specific knowledge, the STN enhances the Proximal Policy Optimization (PPO) algorithm's effectiveness without compromising performance, suggesting its suitability for a wide range of queueing network control problems.

Intervention-Assisted Policy Gradient Methods for Online Stochastic Queuing Network Optimization: Technical Report

Deep Reinforcement Learning (DRL) offers a powerful approach to training neural network control policies for stochastic queuing networks (SQN). However, traditional DRL methods rely on offline simulations or static datasets, limiting their real-world application in SQN control. This work proposes Online Deep Reinforcement Learning-based Controls (ODRLC) as an alternative, where an intelligent agent interacts directly with a real environment and learns an optimal control policy from these online interactions. SQNs present a challenge for ODRLC due to the unbounded nature of the queues within the network resulting in an unbounded state-space. An unbounded state-space is particularly challenging for neural network policies as neural networks are notoriously poor at extrapolating to unseen states. To address this challenge, we propose an intervention-assisted framework that leverages strategic interventions from known stable policies to ensure the queue sizes remain bounded. This framework combines the learning power of neural networks with the guaranteed stability of classical control policies for SQNs. We introduce a method to design these intervention-assisted policies to ensure strong stability of the network. Furthermore, we extend foundational DRL theorems for intervention-assisted policies and develop two practical algorithms specifically for ODRLC of SQNs. Finally, we demonstrate through experiments that our proposed algorithms outperform both classical control approaches and prior ODRLC algorithms.

Learning Algorithms for Minimizing Queue Length Regret

We consider a system consisting of a single transmitter/receiver pair and $N$ channels over which they may communicate. Packets randomly arrive to the transmitter's queue and wait to be successfully sent to the receiver. The transmitter may attempt a frame transmission on one channel at a time, where each frame includes a packet if one is in the queue. For each channel, an attempted transmission is successful with an unknown probability. The transmitter's objective is to quickly identify the best channel to minimize the number of packets in the queue over $T$ time slots. To analyze system performance, we introduce queue length regret, which is the expected difference between the total queue length of a learning policy and a controller that knows the rates, a priori. One approach to designing a transmission policy would be to apply algorithms from the literature that solve the closely-related stochastic multi-armed bandit problem. These policies would focus on maximizing the number of successful frame transmissions over time. However, we show that these methods have $\Omega(\log{T})$ queue length regret. On the other hand, we show that there exists a set of queue-length based policies that can obtain order optimal $O(1)$ queue length regret. We use our theoretical analysis to devise heuristic methods that are shown to perform well in simulation.