Oscillation Reduction for Knuckle Cranes

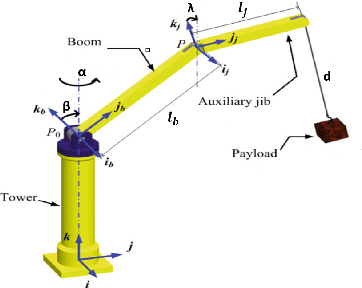
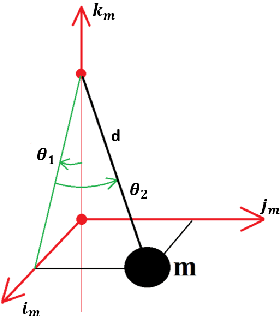
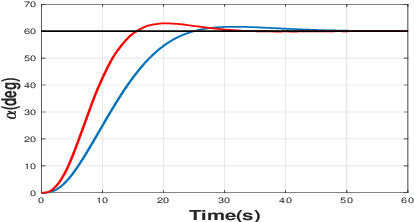
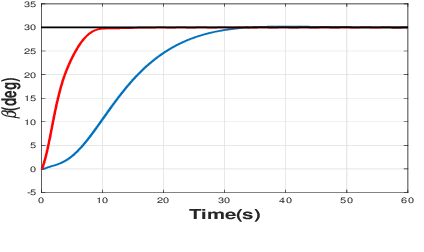
Boom cranes are among the most common material handling systems due to their simple design. Some boom cranes also have an auxiliary jib connected to the boom with a flexible joint to enhance the maneuverability and increase the workspace of the crane. Such boom cranes are commonly called knuckle boom cranes. Due to their underactuated properties, it is fairly challenging to control knuckle boom cranes. To the best of our knowledge, only a few techniques are present in the literature to control this type of cranes using approximate models of the crane. In this paper we present for the first time a complete mathematical model for this crane where it is possible to control the three rotations of the crane (known as luff, slew, and jib movement), and the cable length. One of the main challenges to control this system is how to reduce the oscillations in an effective way. In this paper we propose a nonlinear control based on energy considerations capable of guiding the crane to desired sets points while effectively reducing load oscillations. The corresponding stability and convergence analysis is proved using the LaSalle's invariance principle. Simulation results are provided to demonstrate the effectiveness and feasibility of the proposed method.