Constraint Control of a Boom Crane System

Boom cranes are among the most used cranes to lift heavy loads. Although fairly simple mechanically, from the control viewpoint this kind of crane is a nonlinear underactuated system which presents several challenges, especially when con-trolled in the presence of constraints. To solve this problem, we propose an approach based on the Explicit Reference Governor (ERG), which does not require any online optimization, thus making it computationally inexpensive. The proposed control scheme is able to steer the crane to a desired position ensuring the respect of limited joint ranges, maximum oscillation angle, and the avoidance of static obstacles.

Oscillation Reduction for Knuckle Cranes

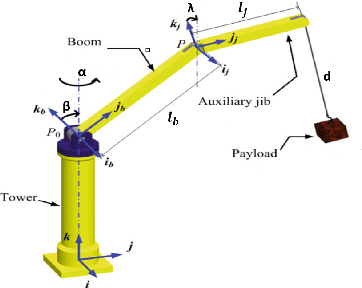
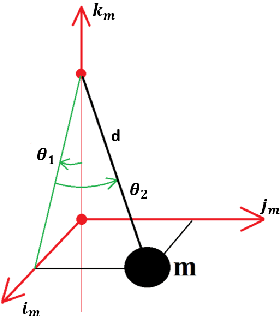
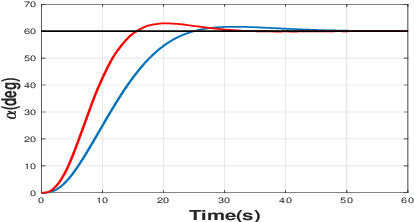
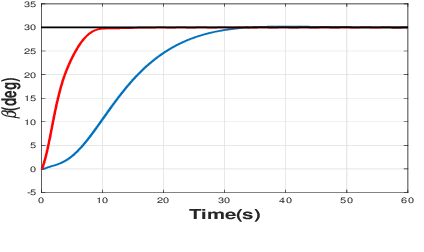
Boom cranes are among the most common material handling systems due to their simple design. Some boom cranes also have an auxiliary jib connected to the boom with a flexible joint to enhance the maneuverability and increase the workspace of the crane. Such boom cranes are commonly called knuckle boom cranes. Due to their underactuated properties, it is fairly challenging to control knuckle boom cranes. To the best of our knowledge, only a few techniques are present in the literature to control this type of cranes using approximate models of the crane. In this paper we present for the first time a complete mathematical model for this crane where it is possible to control the three rotations of the crane (known as luff, slew, and jib movement), and the cable length. One of the main challenges to control this system is how to reduce the oscillations in an effective way. In this paper we propose a nonlinear control based on energy considerations capable of guiding the crane to desired sets points while effectively reducing load oscillations. The corresponding stability and convergence analysis is proved using the LaSalle's invariance principle. Simulation results are provided to demonstrate the effectiveness and feasibility of the proposed method.

Modeling and control of 5-DoF boom crane

Automation of cranes can have a direct impact on the productivity of construction projects. In this paper, we focus on the control of one of the most used cranes, the boom crane. Tower cranes and overhead cranes have been widely studied in the literature, whereas the control of boom cranes has been investigated only by a few works. Typically, these works make use of simple models making use of a large number of simplifying assumptions (e.g. fixed length cable, assuming certain dynamics are uncoupled, etc.) A first result of this paper is to present a fairly complete nonlinear dynamic model of a boom crane taking into account all coupling dynamics and where the only simplifying assumption is that the cable is considered as rigid. The boom crane involves pitching and rotational movements, which generate complicated centrifugal forces, and consequently, equations of motion highly nonlinear. On the basis of this model, a control law has been developed able to perform position control of the crane while actively damping the oscillations of the load. The effectiveness of the approach has been tested in simulation with realistic physical parameters and tested in the presence of wind disturbances.