Brayan Ortiz
Mesh-Based Solutions for Nonparametric Penalized Regression
Dec 07, 2021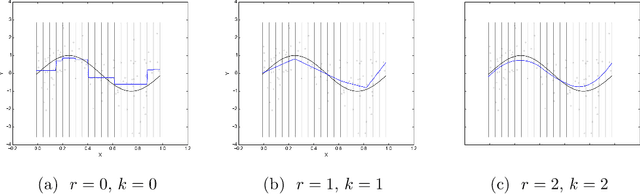
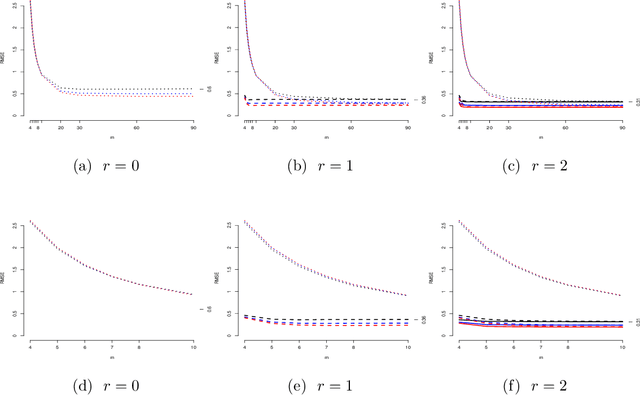
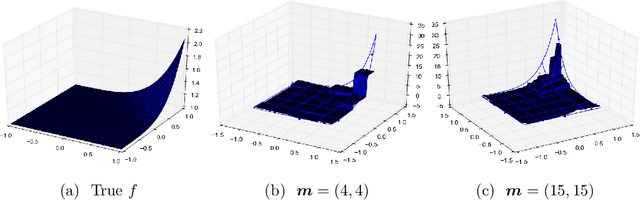
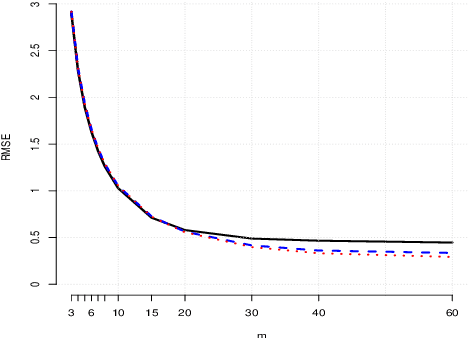
Abstract:It is often of interest to estimate regression functions non-parametrically. Penalized regression (PR) is one statistically-effective, well-studied solution to this problem. Unfortunately, in many cases, finding exact solutions to PR problems is computationally intractable. In this manuscript, we propose a mesh-based approximate solution (MBS) for those scenarios. MBS transforms the complicated functional minimization of NPR, to a finite parameter, discrete convex minimization; and allows us to leverage the tools of modern convex optimization. We show applications of MBS in a number of explicit examples (including both uni- and multi-variate regression), and explore how the number of parameters must increase with our sample-size in order for MBS to maintain the rate-optimality of NPR. We also give an efficient algorithm to minimize the MBS objective while effectively leveraging the sparsity inherent in MBS.
Using Image Transformations to Learn Network Structure
Dec 06, 2021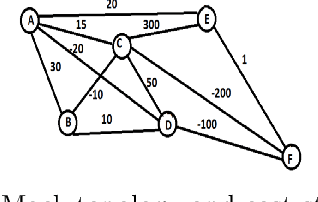

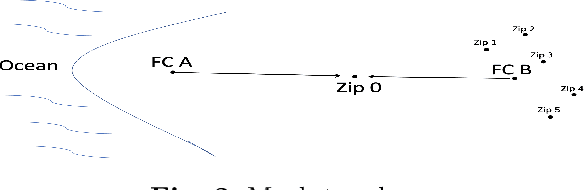
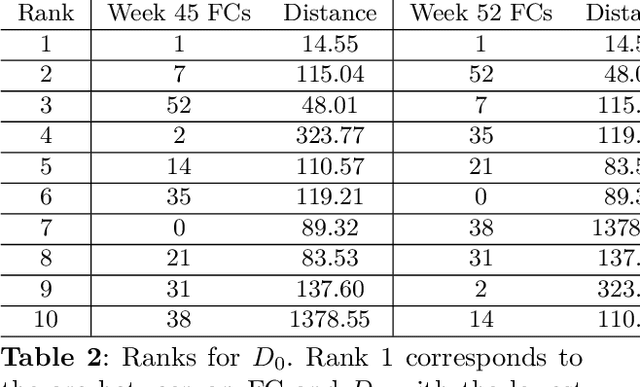
Abstract:Many learning tasks require observing a sequence of images and making a decision. In a transportation problem of designing and planning for shipping boxes between nodes, we show how to treat the network of nodes and the flows between them as images. These images have useful structural information that can be statistically summarized. Using image compression techniques, we reduce an image down to a set of numbers that contain interpretable geographic information that we call geographic signatures. Using geographic signatures, we learn network structure that can be utilized to recommend future network connectivity. We develop a Bayesian reinforcement algorithm that takes advantage of statistically summarized network information as priors and user-decisions to reinforce an agent's probabilistic decision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge