Efficient Guided Generation for Large Language Models

In this article we describe an efficient approach to guiding language model text generation with regular expressions and context-free grammars. Our approach adds little to no overhead to the token sequence generation process, and makes guided generation feasible in practice. An implementation is provided in the open source Python library Outlines.

A Statistical Theory of Deep Learning via Proximal Splitting

In this paper we develop a statistical theory and an implementation of deep learning models. We show that an elegant variable splitting scheme for the alternating direction method of multipliers optimises a deep learning objective. We allow for non-smooth non-convex regularisation penalties to induce sparsity in parameter weights. We provide a link between traditional shallow layer statistical models such as principal component and sliced inverse regression and deep layer models. We also define the degrees of freedom of a deep learning predictor and a predictive MSE criteria to perform model selection for comparing architecture designs. We focus on deep multiclass logistic learning although our methods apply more generally. Our results suggest an interesting and previously under-exploited relationship between deep learning and proximal splitting techniques. To illustrate our methodology, we provide a multi-class logit classification analysis of Fisher's Iris data where we illustrate the convergence of our algorithm. Finally, we conclude with directions for future research.

Proximal Algorithms in Statistics and Machine Learning

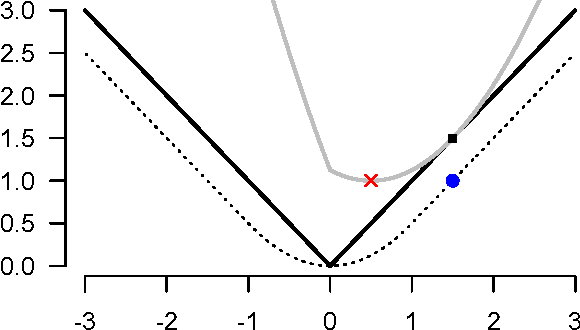
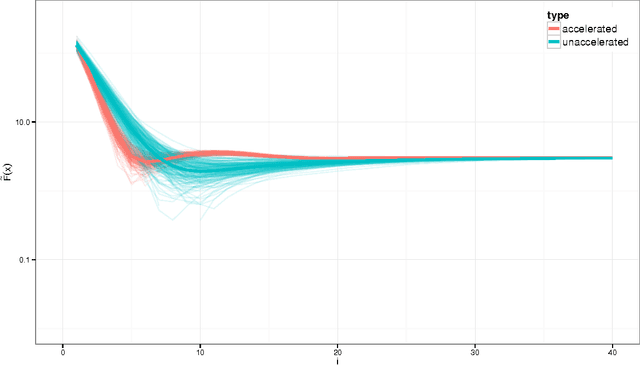
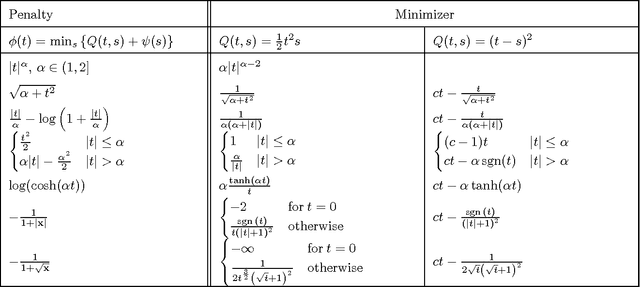
In this paper we develop proximal methods for statistical learning. Proximal point algorithms are useful in statistics and machine learning for obtaining optimization solutions for composite functions. Our approach exploits closed-form solutions of proximal operators and envelope representations based on the Moreau, Forward-Backward, Douglas-Rachford and Half-Quadratic envelopes. Envelope representations lead to novel proximal algorithms for statistical optimisation of composite objective functions which include both non-smooth and non-convex objectives. We illustrate our methodology with regularized Logistic and Poisson regression and non-convex bridge penalties with a fused lasso norm. We provide a discussion of convergence of non-descent algorithms with acceleration and for non-convex functions. Finally, we provide directions for future research.