Adaptive sparse variational approximations for Gaussian process regression

Accurate tuning of hyperparameters is crucial to ensure that models can generalise effectively across different settings. In this paper, we present theoretical guarantees for hyperparameter selection using variational Bayes in the nonparametric regression model. We construct a variational approximation to a hierarchical Bayes procedure, and derive upper bounds for the contraction rate of the variational posterior in an abstract setting. The theory is applied to various Gaussian process priors and variational classes, resulting in minimax optimal rates. Our theoretical results are accompanied with numerical analysis both on synthetic and real world data sets.

Distributed Nonparametric Estimation under Communication Constraints

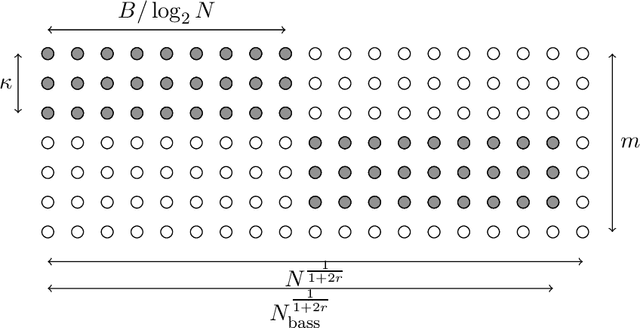
In the era of big data, it is necessary to split extremely large data sets across multiple computing nodes and construct estimators using the distributed data. When designing distributed estimators, it is desirable to minimize the amount of communication across the network because transmission between computers is slow in comparison to computations in a single computer. Our work provides a general framework for understanding the behavior of distributed estimation under communication constraints for nonparametric problems. We provide results for a broad class of models, moving beyond the Gaussian framework that dominates the literature. As concrete examples we derive minimax lower and matching upper bounds in the distributed regression, density estimation, classification, Poisson regression and volatility estimation models under communication constraints. To assist with this, we provide sufficient conditions that can be easily verified in all of our examples.

Optimal high-dimensional and nonparametric distributed testing under communication constraints

We derive minimax testing errors in a distributed framework where the data is split over multiple machines and their communication to a central machine is limited to $b$ bits. We investigate both the $d$- and infinite-dimensional signal detection problem under Gaussian white noise. We also derive distributed testing algorithms reaching the theoretical lower bounds. Our results show that distributed testing is subject to fundamentally different phenomena that are not observed in distributed estimation. Among our findings, we show that testing protocols that have access to shared randomness can perform strictly better in some regimes than those that do not. Furthermore, we show that consistent nonparametric distributed testing is always possible, even with as little as $1$-bit of communication and the corresponding test outperforms the best local test using only the information available at a single local machine.