Pseudo-Boolean Polynomials Approach To Edge Detection And Image Segmentation

We introduce a deterministic approach to edge detection and image segmentation by formulating pseudo-Boolean polynomials on image patches. The approach works by applying a binary classification of blob and edge regions in an image based on the degrees of pseudo-Boolean polynomials calculated on patches extracted from the provided image. We test our method on simple images containing primitive shapes of constant and contrasting colour and establish the feasibility before applying it to complex instances like aerial landscape images. The proposed method is based on the exploitation of the reduction, polynomial degree, and equivalence properties of penalty-based pseudo-Boolean polynomials.

A Pseudo-Boolean Polynomials Approach for Image Edge Detection

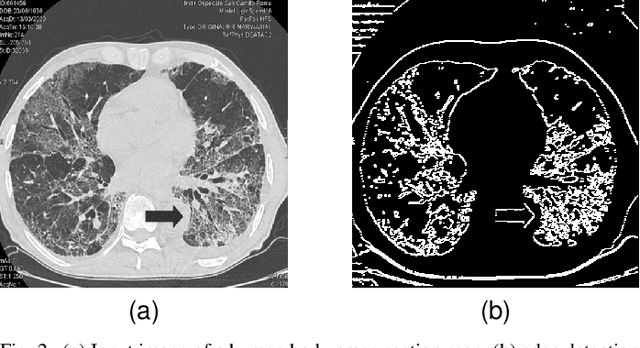
We introduce a novel approach for image edge detection based on pseudo-Boolean polynomials for image patches. We show that patches covering edge regions in the image result in pseudo-Boolean polynomials with higher degrees compared to patches that cover blob regions. The proposed approach is based on reduction of polynomial degree and equivalence properties of penalty-based pseudo-Boolean polynomials.

Dimensionality Reduction Using pseudo-Boolean polynomials For Cluster Analysis

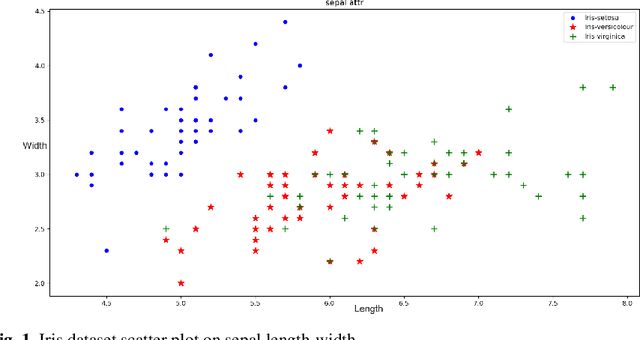
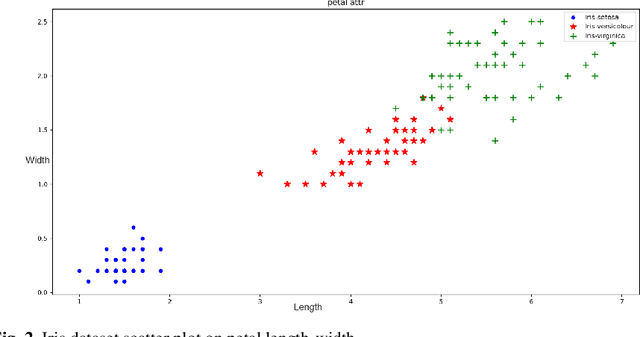
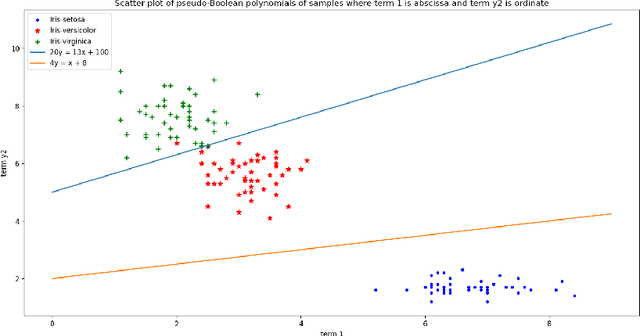
We introduce usage of a reduction property of penalty-based formulation of pseudo-Boolean polynomials as a mechanism for invariant dimensionality reduction in cluster analysis processes. In our experiments, we show that multidimensional data, like 4-dimensional Iris Flower dataset can be reduced to 2-dimensional space while the 30-dimensional Wisconsin Diagnostic Breast Cancer (WDBC) dataset can be reduced to 3-dimensional space, and by searching lines or planes that lie between reduced samples we can extract clusters in a linear and unbiased manner with competitive accuracies, reproducibility and clear interpretation.

Conditional Markov Chain Search for the Simple Plant Location Problem improves upper bounds on twelve Körkel-Ghosh instances

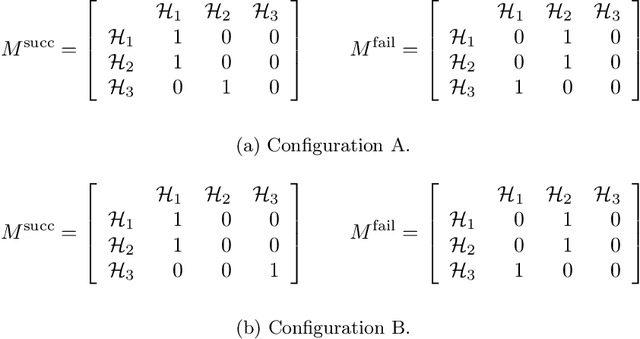
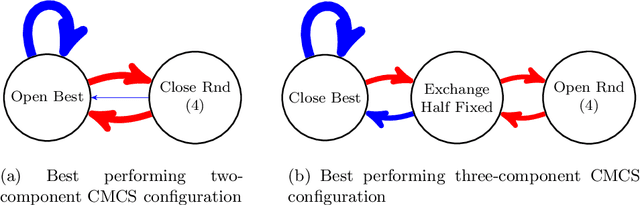
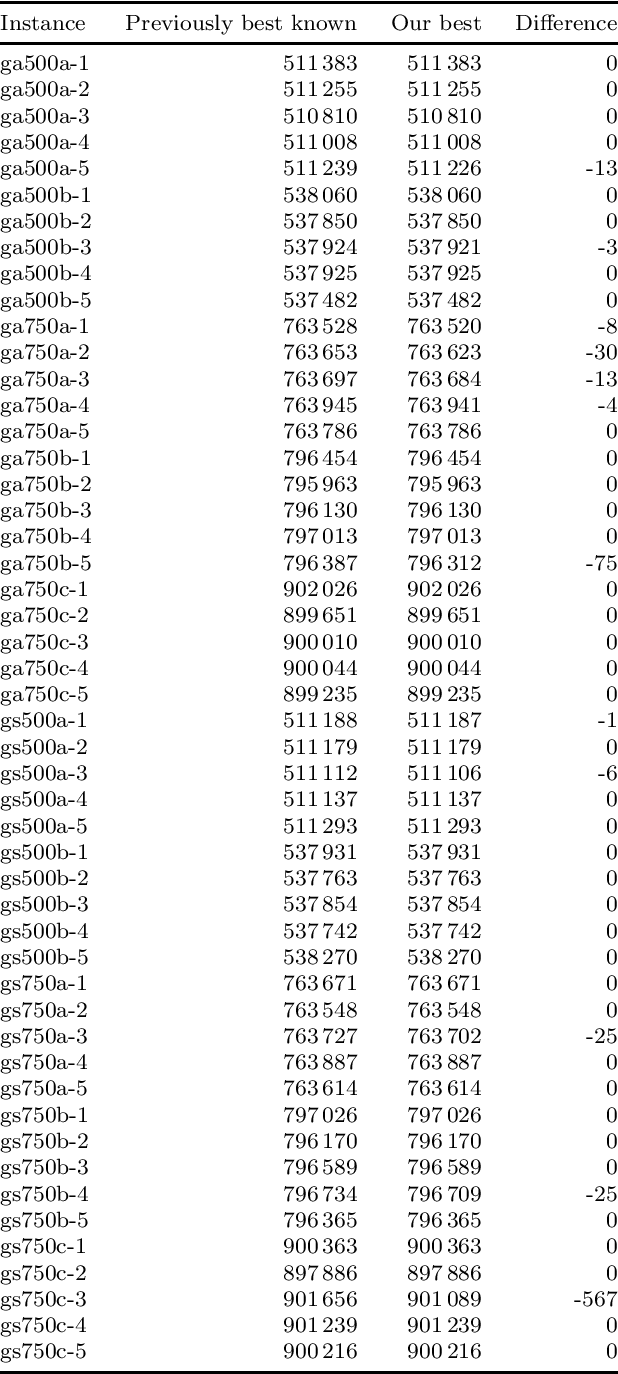
We address a family of hard benchmark instances for the Simple Plant Location Problem (also known as the Uncapacitated Facility Location Problem). The recent attempt by Fischetti et al. to tackle the K\"orkel-Ghosh instances resulted in seven new optimal solutions and 22 improved upper bounds. We use automated generation of heuristics to obtain a new algorithm for the Simple Plant Location Problem. In our experiments, our new algorithm matched all the previous best known and optimal solutions, and further improved 12 upper bounds, all within shorter time budgets compared to the previous efforts. Our algorithm design process is split into two phases: (i) development of algorithmic components such as local search procedures and mutation operators, and (ii) composition of a metaheuristic from the available components. Phase (i) requires human expertise and often can be completed by implementing several simple domain-specific routines known from the literature. Phase (ii) is entirely automated by employing the Conditional Markov Chain Search (CMCS) framework. In CMCS, a metaheuristic is flexibly defined by a set of parameters, called configuration. Then the process of composition of a metaheuristic from the algorithmic components is reduced to an optimisation problem seeking the best performing CMCS configuration. We discuss the problem of comparing configurations, and propose a new efficient technique to select the best performing configuration from a large set. To employ this method, we restrict the original CMCS to a simple deterministic case that leaves us with a finite and manageable number of meaningful configurations.