Pseudo-Boolean Polynomials Approach To Edge Detection And Image Segmentation

We introduce a deterministic approach to edge detection and image segmentation by formulating pseudo-Boolean polynomials on image patches. The approach works by applying a binary classification of blob and edge regions in an image based on the degrees of pseudo-Boolean polynomials calculated on patches extracted from the provided image. We test our method on simple images containing primitive shapes of constant and contrasting colour and establish the feasibility before applying it to complex instances like aerial landscape images. The proposed method is based on the exploitation of the reduction, polynomial degree, and equivalence properties of penalty-based pseudo-Boolean polynomials.

A Pseudo-Boolean Polynomials Approach for Image Edge Detection

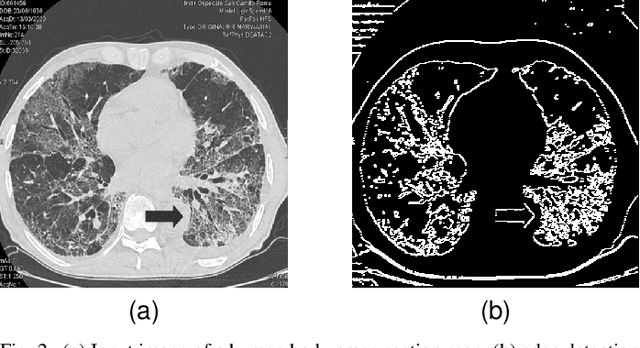
We introduce a novel approach for image edge detection based on pseudo-Boolean polynomials for image patches. We show that patches covering edge regions in the image result in pseudo-Boolean polynomials with higher degrees compared to patches that cover blob regions. The proposed approach is based on reduction of polynomial degree and equivalence properties of penalty-based pseudo-Boolean polynomials.

Dimensionality Reduction Using pseudo-Boolean polynomials For Cluster Analysis

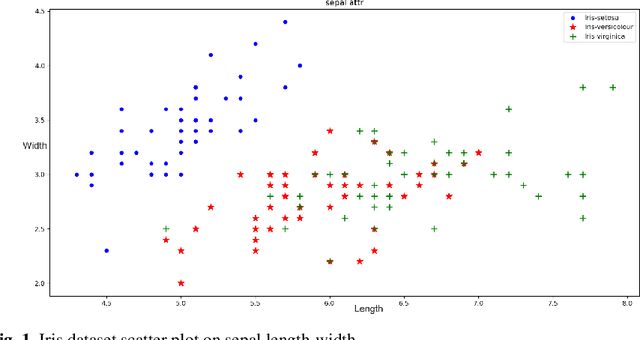
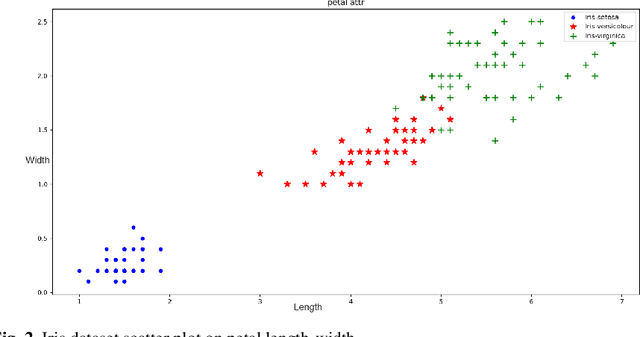
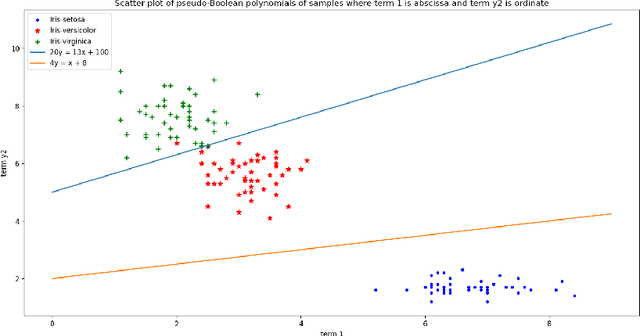
We introduce usage of a reduction property of penalty-based formulation of pseudo-Boolean polynomials as a mechanism for invariant dimensionality reduction in cluster analysis processes. In our experiments, we show that multidimensional data, like 4-dimensional Iris Flower dataset can be reduced to 2-dimensional space while the 30-dimensional Wisconsin Diagnostic Breast Cancer (WDBC) dataset can be reduced to 3-dimensional space, and by searching lines or planes that lie between reduced samples we can extract clusters in a linear and unbiased manner with competitive accuracies, reproducibility and clear interpretation.