FAIR: Fair Adversarial Instance Re-weighting

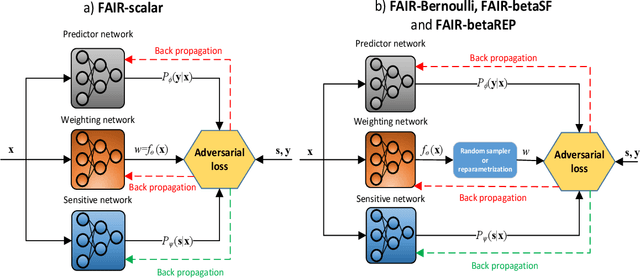
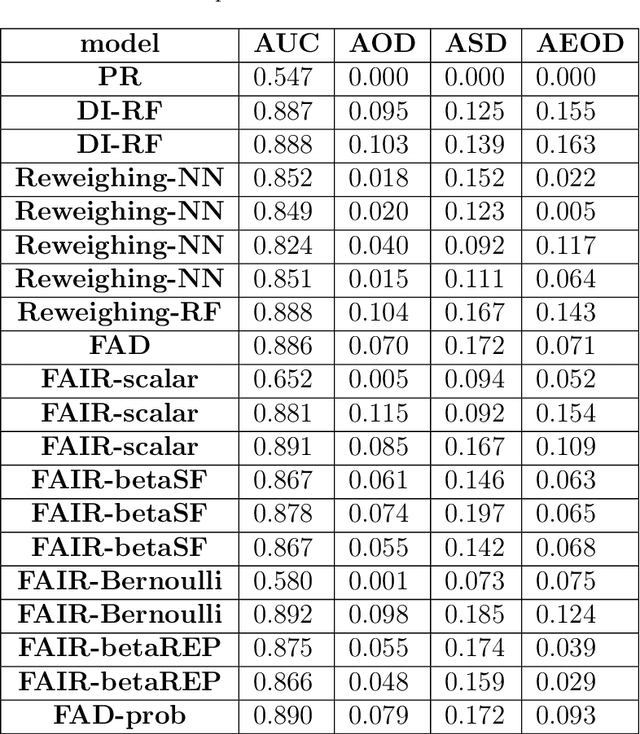
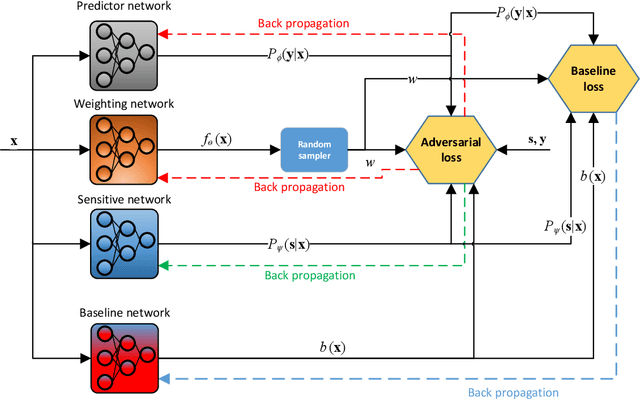
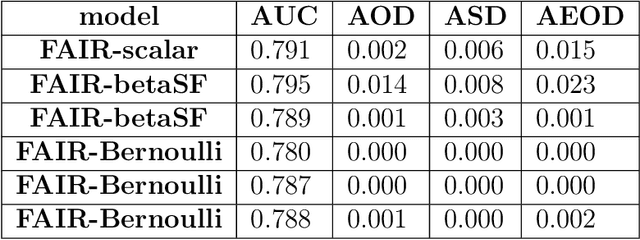
With growing awareness of societal impact of artificial intelligence, fairness has become an important aspect of machine learning algorithms. The issue is that human biases towards certain groups of population, defined by sensitive features like race and gender, are introduced to the training data through data collection and labeling. Two important directions of fairness ensuring research have focused on (i) instance weighting in order to decrease the impact of more biased instances and (ii) adversarial training in order to construct data representations informative of the target variable, but uninformative of the sensitive attributes. In this paper we propose a Fair Adversarial Instance Re-weighting (FAIR) method, which uses adversarial training to learn instance weighting function that ensures fair predictions. Merging the two paradigms, it inherits desirable properties from both -- interpretability of reweighting and end-to-end trainability of adversarial training. We propose four different variants of the method and, among other things, demonstrate how the method can be cast in a fully probabilistic framework. Additionally, theoretical analysis of FAIR models' properties have been studied extensively. We compare FAIR models to 7 other related and state-of-the-art models and demonstrate that FAIR is able to achieve a better trade-off between accuracy and unfairness. To the best of our knowledge, this is the first model that merges reweighting and adversarial approaches by means of a weighting function that can provide interpretable information about fairness of individual instances.

Gaussian Conditional Random Fields for Classification

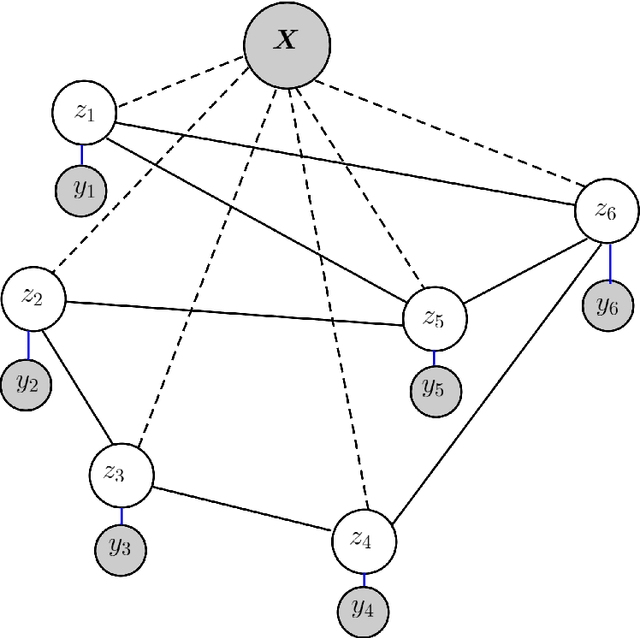
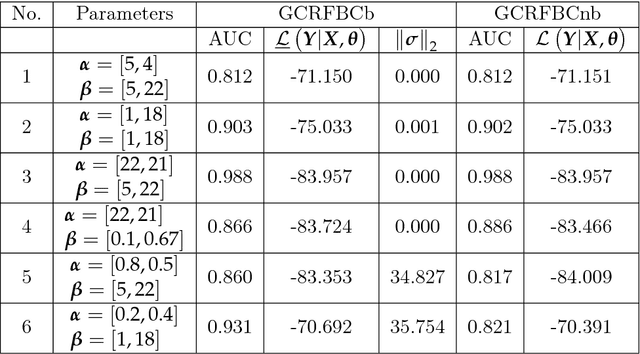
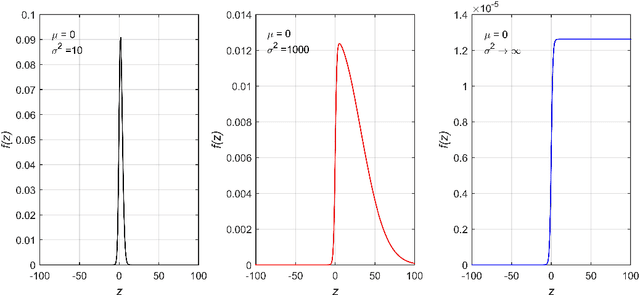
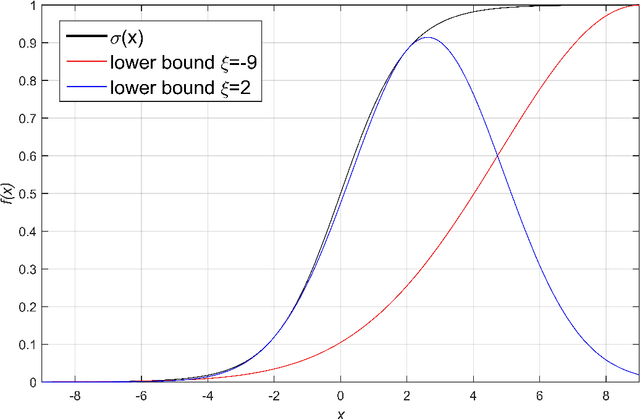
Gaussian conditional random fields (GCRF) are a well-known used structured model for continuous outputs that uses multiple unstructured predictors to form its features and at the same time exploits dependence structure among outputs, which is provided by a similarity measure. In this paper, a Gaussian conditional random fields model for structured binary classification (GCRFBC) is proposed. The model is applicable to classification problems with undirected graphs, intractable for standard classification CRFs. The model representation of GCRFBC is extended by latent variables which yield some appealing properties. Thanks to the GCRF latent structure, the model becomes tractable, efficient and open to improvements previously applied to GCRF regression models. In addition, the model allows for reduction of noise, that might appear if structures were defined directly between discrete outputs. Additionally, two different forms of the algorithm are presented: GCRFBCb (GCRGBC - Bayesian) and GCRFBCnb (GCRFBC - non Bayesian). The extended method of local variational approximation of sigmoid function is used for solving empirical Bayes in Bayesian GCRFBCb variant, whereas MAP value of latent variables is the basis for learning and inference in the GCRFBCnb variant. The inference in GCRFBCb is solved by Newton-Cotes formulas for one-dimensional integration. Both models are evaluated on synthetic data and real-world data. It was shown that both models achieve better prediction performance than unstructured predictors. Furthermore, computational and memory complexity is evaluated. Advantages and disadvantages of the proposed GCRFBCb and GCRFBCnb are discussed in detail.