Gaussian Conditional Random Fields for Classification
Paper and Code
Jan 31, 2019
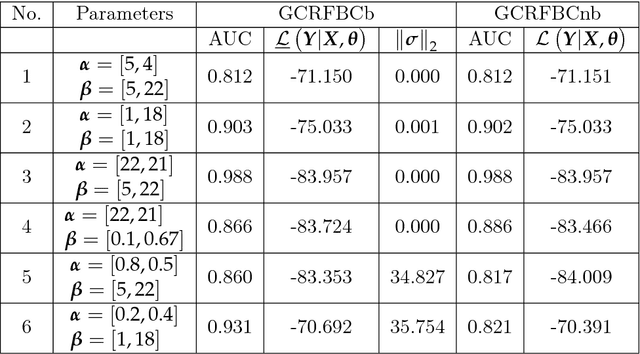
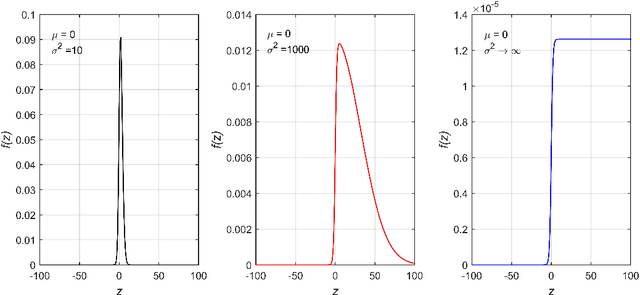
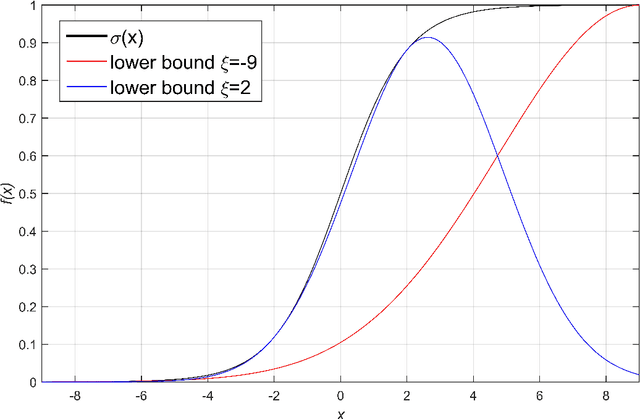
Gaussian conditional random fields (GCRF) are a well-known used structured model for continuous outputs that uses multiple unstructured predictors to form its features and at the same time exploits dependence structure among outputs, which is provided by a similarity measure. In this paper, a Gaussian conditional random fields model for structured binary classification (GCRFBC) is proposed. The model is applicable to classification problems with undirected graphs, intractable for standard classification CRFs. The model representation of GCRFBC is extended by latent variables which yield some appealing properties. Thanks to the GCRF latent structure, the model becomes tractable, efficient and open to improvements previously applied to GCRF regression models. In addition, the model allows for reduction of noise, that might appear if structures were defined directly between discrete outputs. Additionally, two different forms of the algorithm are presented: GCRFBCb (GCRGBC - Bayesian) and GCRFBCnb (GCRFBC - non Bayesian). The extended method of local variational approximation of sigmoid function is used for solving empirical Bayes in Bayesian GCRFBCb variant, whereas MAP value of latent variables is the basis for learning and inference in the GCRFBCnb variant. The inference in GCRFBCb is solved by Newton-Cotes formulas for one-dimensional integration. Both models are evaluated on synthetic data and real-world data. It was shown that both models achieve better prediction performance than unstructured predictors. Furthermore, computational and memory complexity is evaluated. Advantages and disadvantages of the proposed GCRFBCb and GCRFBCnb are discussed in detail.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge