Contrastive Learning and Mixture of Experts Enables Precise Vector Embeddings

The advancement of transformer neural networks has significantly elevated the capabilities of sentence similarity models, particularly in creating effective vector representations of natural language inputs. However, these models face notable challenges in domain-specific contexts, especially in highly specialized scientific sub-fields. Traditional methods often struggle in this regime, either overgeneralizing similarities within a niche or being overly sensitive to minor differences, resulting in inaccurate text classification and subpar vector representation. In an era where retrieval augmentation and search are increasingly crucial, precise and concise numerical representations are essential. In this paper, we target this issue by assembling niche datasets using co-citations as a similarity metric, focusing on biomedical domains. We employ two key strategies for fine-tuning state-of-the-art models: 1. Domain-specific Fine-Tuning, which tailors pretrained models to a single domain, and 2. Universal Applicability with Mixture of Experts (MoE), adapting pretrained models with enforced routing for multiple domains simultaneously. Our training approach emphasizes the use of abstracts for faster training, incorporating Multiple Negative Rankings loss for efficient contrastive learning. Notably, our MoE variants, equipped with $N$ experts, achieve the efficacy of $N$ individual models, heralding a new era of versatile, One-Size-Fits-All transformer networks for various tasks. This methodology marks significant advancements in scientific text classification metrics and holds promise for enhancing vector database search and compilation.

Modeling natural language emergence with integral transform theory and reinforcement learning

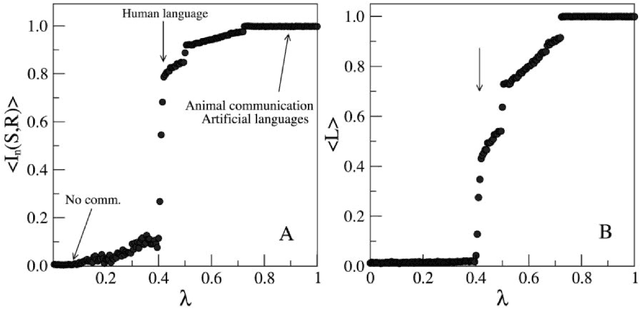
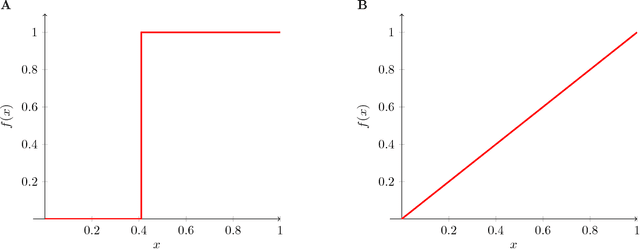
Zipf's law predicts a power-law relationship between word rank and frequency in language communication systems and has been widely reported in a variety of natural language processing applications. However, the emergence of natural language is often modeled as a function of bias between speaker and listener interests, which lacks a direct way of relating information-theoretic bias to Zipfian rank. A function of bias also serves as an unintuitive interpretation of the communicative effort exchanged between a speaker and a listener. We counter these shortcomings by proposing a novel integral transform and kernel for mapping communicative bias functions to corresponding word frequency-rank representations at any arbitrary phase transition point, resulting in a direct way to link communicative effort (modeled by speaker/listener bias) to specific vocabulary used (represented by word rank). We demonstrate the practical utility of our integral transform by showing how a change from bias to rank results in greater accuracy and performance at an image classification task for assigning word labels to images randomly subsampled from CIFAR10. We model this task as a reinforcement learning game between a speaker and listener and compare the relative impact of bias and Zipfian word rank on communicative performance (and accuracy) between the two agents.

Polynomial Regression As an Alternative to Neural Nets

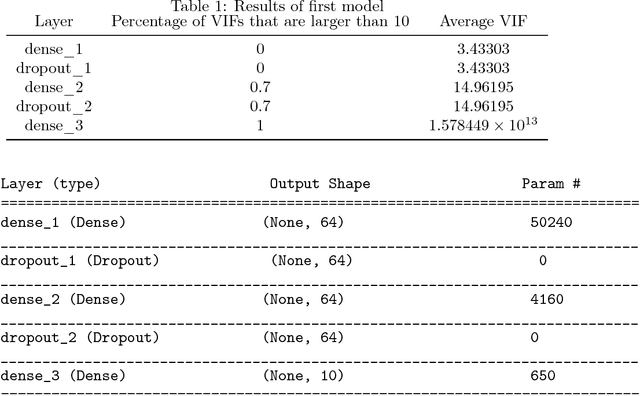
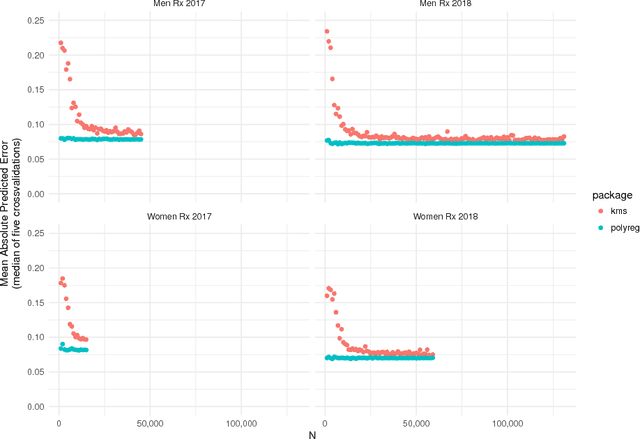
Despite the success of neural networks (NNs), there is still a concern among many over their "black box" nature. Why do they work? Here we present a simple analytic argument that NNs are in fact essentially polynomial regression models. This view will have various implications for NNs, e.g. providing an explanation for why convergence problems arise in NNs, and it gives rough guidance on avoiding overfitting. In addition, we use this phenomenon to predict and confirm a multicollinearity property of NNs not previously reported in the literature. Most importantly, given this loose correspondence, one may choose to routinely use polynomial models instead of NNs, thus avoiding some major problems of the latter, such as having to set many tuning parameters and dealing with convergence issues. We present a number of empirical results; in each case, the accuracy of the polynomial approach matches or exceeds that of NN approaches. A many-featured, open-source software package, polyreg, is available.