Active Learning in Genetic Programming: Guiding Efficient Data Collection for Symbolic Regression

This paper examines various methods of computing uncertainty and diversity for active learning in genetic programming. We found that the model population in genetic programming can be exploited to select informative training data points by using a model ensemble combined with an uncertainty metric. We explored several uncertainty metrics and found that differential entropy performed the best. We also compared two data diversity metrics and found that correlation as a diversity metric performs better than minimum Euclidean distance, although there are some drawbacks that prevent correlation from being used on all problems. Finally, we combined uncertainty and diversity using a Pareto optimization approach to allow both to be considered in a balanced way to guide the selection of informative and unique data points for training.

Correlation versus RMSE Loss Functions in Symbolic Regression Tasks

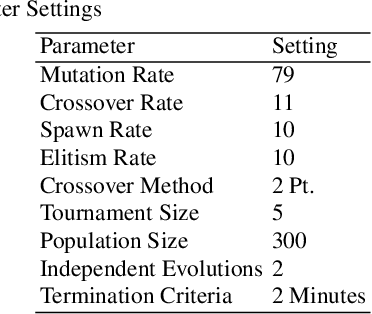
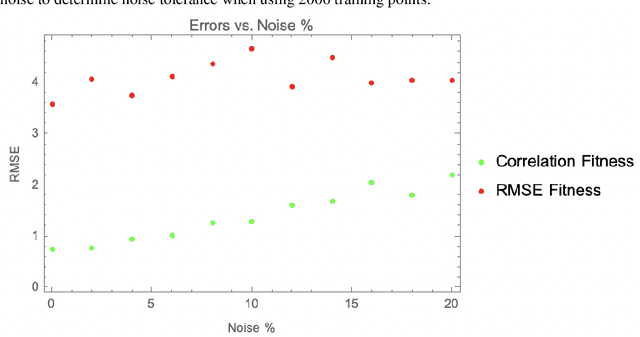
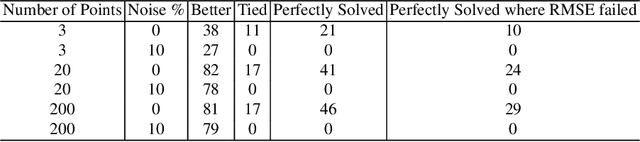
The use of correlation as a fitness function is explored in symbolic regression tasks and the performance is compared against the typical RMSE fitness function. Using correlation with an alignment step to conclude the evolution led to significant performance gains over RMSE as a fitness function. Using correlation as a fitness function led to solutions being found in fewer generations compared to RMSE, as well it was found that fewer data points were needed in the training set to discover the correct equations. The Feynman Symbolic Regression Benchmark as well as several other old and recent GP benchmark problems were used to evaluate performance.

Active Learning Improves Performance on Symbolic RegressionTasks in StackGP

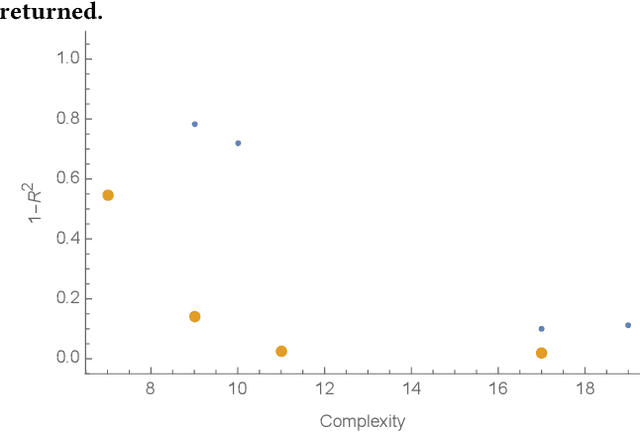
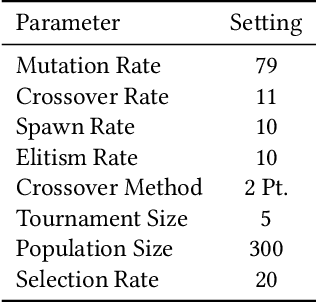
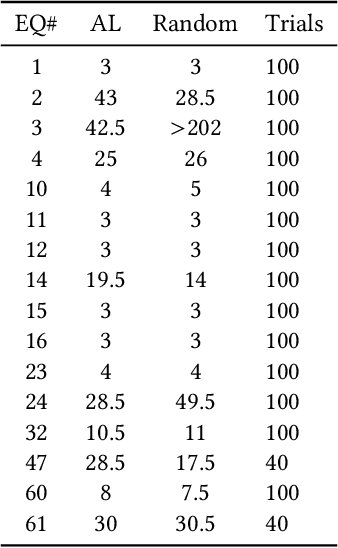
In this paper we introduce an active learning method for symbolic regression using StackGP. The approach begins with a small number of data points for StackGP to model. To improve the model the system incrementally adds a data point such that the new point maximizes prediction uncertainty as measured by the model ensemble. Symbolic regression is re-run with the larger data set. This cycle continues until the system satisfies a termination criterion. We use the Feynman AI benchmark set of equations to examine the ability of our method to find appropriate models using fewer data points. The approach was found to successfully rediscover 72 of the 100 Feynman equations using as few data points as possible, and without use of domain expertise or data translation.