Benjamin Kap
Causal Identification with Additive Noise Models: Quantifying the Effect of Noise
Oct 15, 2021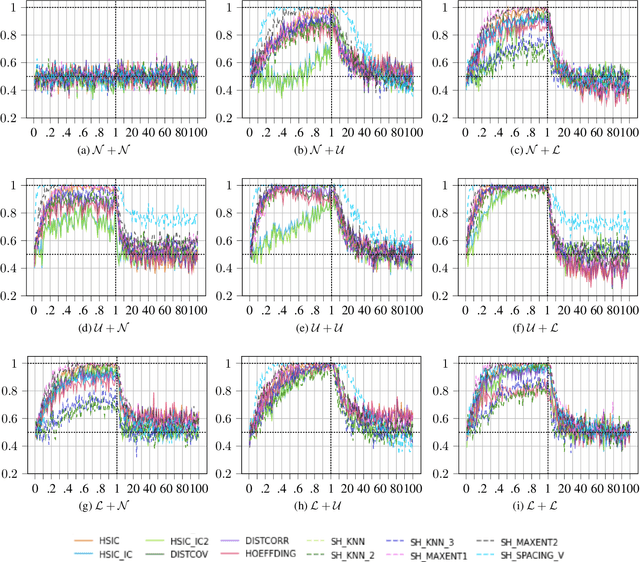

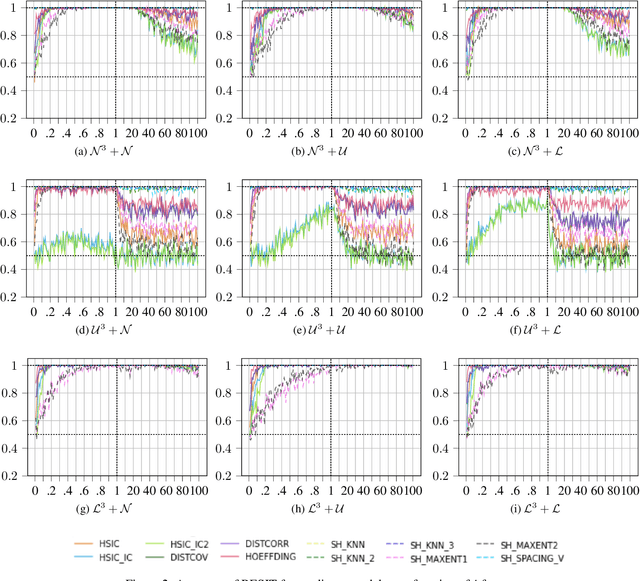

Abstract:In recent years, a lot of research has been conducted within the area of causal inference and causal learning. Many methods have been developed to identify the cause-effect pairs in models and have been successfully applied to observational real-world data to determine the direction of causal relationships. Yet in bivariate situations, causal discovery problems remain challenging. One class of such methods, that also allows tackling the bivariate case, is based on Additive Noise Models (ANMs). Unfortunately, one aspect of these methods has not received much attention until now: what is the impact of different noise levels on the ability of these methods to identify the direction of the causal relationship. This work aims to bridge this gap with the help of an empirical study. We test Regression with Subsequent Independence Test (RESIT) using an exhaustive range of models where the level of additive noise gradually changes from 1\% to 10000\% of the causes' noise level (the latter remains fixed). Additionally, the experiments in this work consider several different types of distributions as well as linear and non-linear models. The results of the experiments show that ANMs methods can fail to capture the true causal direction for some levels of noise.
The Effect of Noise Level on Causal Identification with Additive Noise Models
Aug 24, 2021



Abstract:In recent years a lot of research has been conducted within the area of causal inference and causal learning. Many methods have been developed to identify the cause-effect pairs in models and have been successfully applied to observational real-world data in order to determine the direction of causal relationships. Many of these methods require simplifying assumptions, such as absence of confounding, cycles, and selection bias. Yet in bivariate situations causal discovery problems remain challenging. One class of such methods, that also allows tackling the bivariate case, is based on Additive Noise Models (ANMs). Unfortunately, one aspect of these methods has not received much attention until now: what is the impact of different noise levels on the ability of these methods to identify the direction of the causal relationship. This work aims to bridge this gap with the help of an empirical study. For this work, we considered bivariate cases, which is the most elementary form of a causal discovery problem where one needs to decide whether X causes Y or Y causes X, given joint distributions of two variables X, Y. Furthermore, two specific methods have been selected, \textit{Regression with Subsequent Independence Test} and \textit{Identification using Conditional Variances}, which have been tested with an exhaustive range of ANMs where the additive noises' levels gradually change from 1% to 10000% of the causes' noise level (the latter remains fixed). Additionally, the experiments in this work consider several different types of distributions as well as linear and non-linear ANMs. The results of the experiments show that these methods can fail to capture the true causal direction for some levels of noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge