Benchmarking a wide range of optimisers for solving the Fermi-Hubbard model using the variational quantum eigensolver

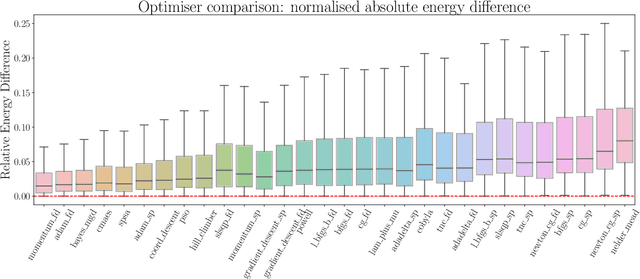
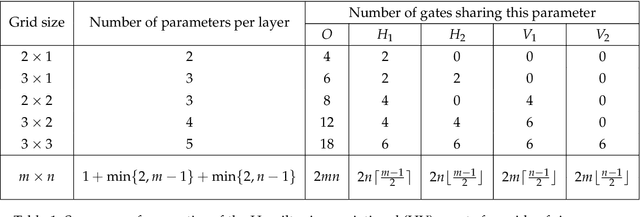
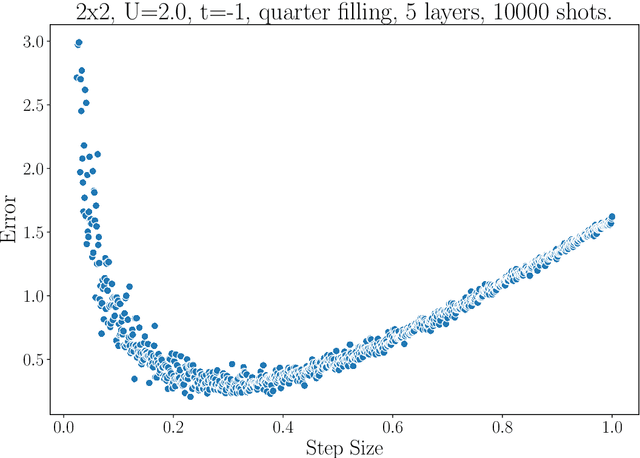
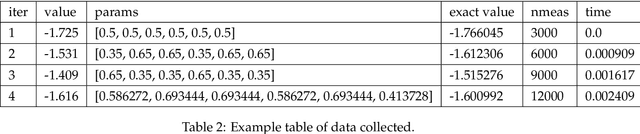
We numerically benchmark 30 optimisers on 372 instances of the variational quantum eigensolver for solving the Fermi-Hubbard system with the Hamiltonian variational ansatz. We rank the optimisers with respect to metrics such as final energy achieved and function calls needed to get within a certain tolerance level, and find that the best performing optimisers are variants of gradient descent such as Momentum and ADAM (using finite difference), SPSA, CMAES, and BayesMGD. We also perform gradient analysis and observe that the step size for finite difference has a very significant impact. We also consider using simultaneous perturbation (inspired by SPSA) as a gradient subroutine: here finite difference can lead to a more precise estimate of the ground state but uses more calls, whereas simultaneous perturbation can converge quicker but may be less precise in the later stages. Finally, we also study the quantum natural gradient algorithm: we implement this method for 1-dimensional Fermi-Hubbard systems, and find that whilst it can reach a lower energy with fewer iterations, this improvement is typically lost when taking total function calls into account. Our method involves performing careful hyperparameter sweeping on 4 instances. We present a variety of analysis and figures, detailed optimiser notes, and discuss future directions.

Optimising Trotter-Suzuki Decompositions for Quantum Simulation Using Evolutionary Strategies

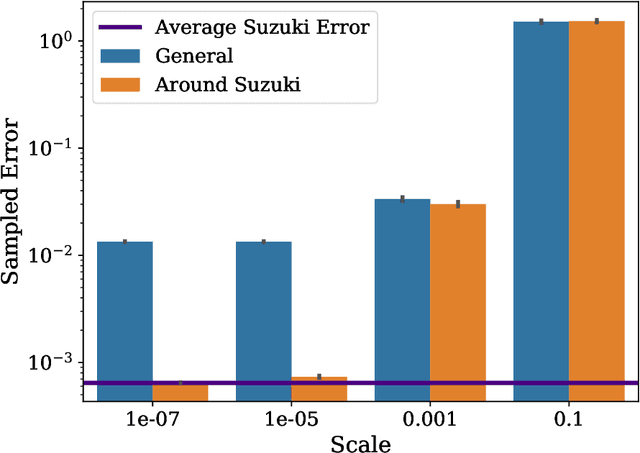
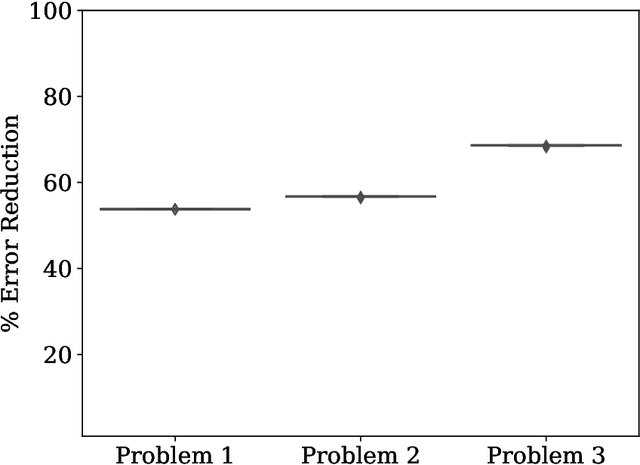
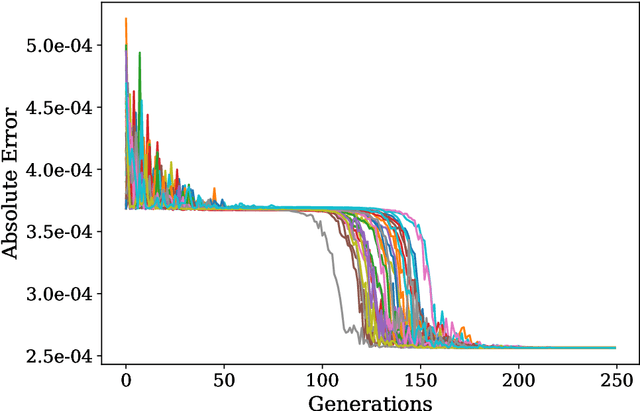
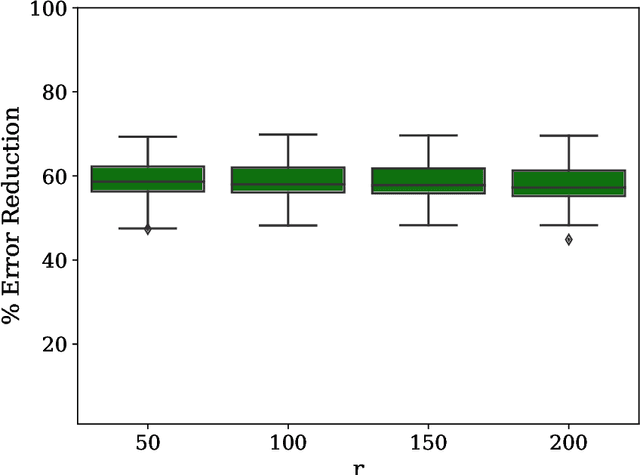
One of the most promising applications of near-term quantum computing is the simulation of quantum systems, a classically intractable task. Quantum simulation requires computationally expensive matrix exponentiation; Trotter-Suzuki decomposition of this exponentiation enables efficient simulation to a desired accuracy on a quantum computer. We apply the Covariance Matrix Adaptation Evolutionary Strategy (CMA-ES) algorithm to optimise the Trotter-Suzuki decompositions of a canonical quantum system, the Heisenberg Chain; we reduce simulation error by around 60%. We introduce this problem to the computational search community, show that an evolutionary optimisation approach is robust across runs and problem instances, and find that optimisation results generalise to the simulation of larger systems.