Benchmarking a wide range of optimisers for solving the Fermi-Hubbard model using the variational quantum eigensolver

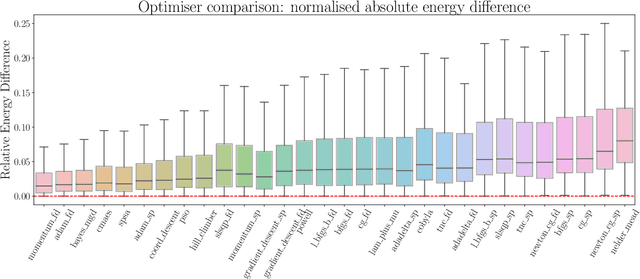
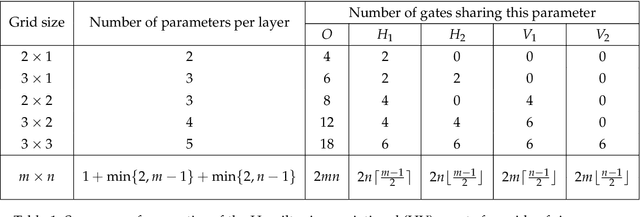
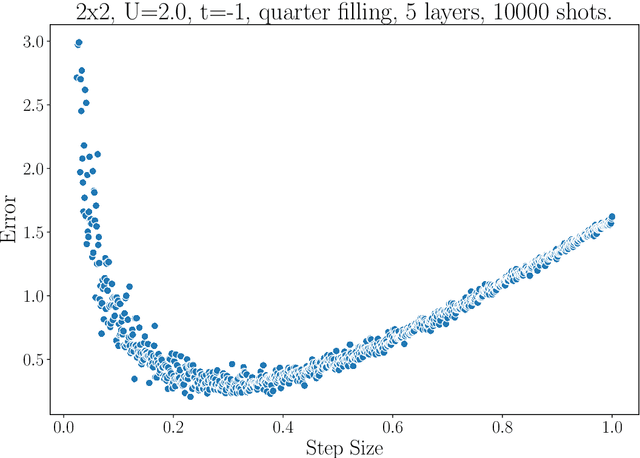
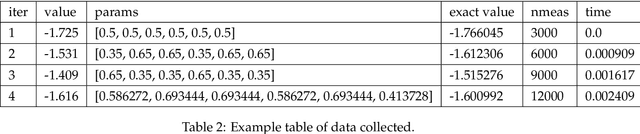
We numerically benchmark 30 optimisers on 372 instances of the variational quantum eigensolver for solving the Fermi-Hubbard system with the Hamiltonian variational ansatz. We rank the optimisers with respect to metrics such as final energy achieved and function calls needed to get within a certain tolerance level, and find that the best performing optimisers are variants of gradient descent such as Momentum and ADAM (using finite difference), SPSA, CMAES, and BayesMGD. We also perform gradient analysis and observe that the step size for finite difference has a very significant impact. We also consider using simultaneous perturbation (inspired by SPSA) as a gradient subroutine: here finite difference can lead to a more precise estimate of the ground state but uses more calls, whereas simultaneous perturbation can converge quicker but may be less precise in the later stages. Finally, we also study the quantum natural gradient algorithm: we implement this method for 1-dimensional Fermi-Hubbard systems, and find that whilst it can reach a lower energy with fewer iterations, this improvement is typically lost when taking total function calls into account. Our method involves performing careful hyperparameter sweeping on 4 instances. We present a variety of analysis and figures, detailed optimiser notes, and discuss future directions.

Designing quantum experiments with a genetic algorithm

We introduce a genetic algorithm that designs quantum optics experiments for engineering quantum states with specific properties. Our algorithm is powerful and flexible, and can easily be modified to find methods of engineering states for a range of applications. Here we focus on quantum metrology. First, we consider the noise-free case, and use the algorithm to find quantum states with a large quantum Fisher information (QFI). We find methods, which only involve experimental elements that are available with current technology, for engineering quantum states with up to a 100-fold improvement over the best classical state, and a 20-fold improvement over the optimal Gaussian state. Such states are a superposition of the vacuum with a large number of photons (around 80), and can hence be seen as Schr\"odinger-cat-like states. We then apply the two most dominant noise sources in our setting -- photon loss and imperfect heralding -- and use the algorithm to find quantum states that still improve over the optimal Gaussian state with realistic levels of noise. This will open up experimental and technological work in using exotic non-Gaussian states for quantum-enhanced phase measurements. Finally, we use the Bayesian mean square error to look beyond the regime of validity of the QFI, finding quantum states with precision enhancements over the alternatives even when the experiment operates in the regime of limited data.