Optimising Trotter-Suzuki Decompositions for Quantum Simulation Using Evolutionary Strategies
Paper and Code
Apr 23, 2019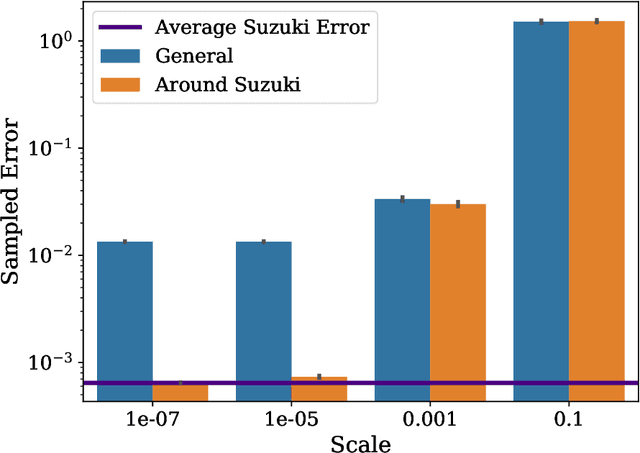
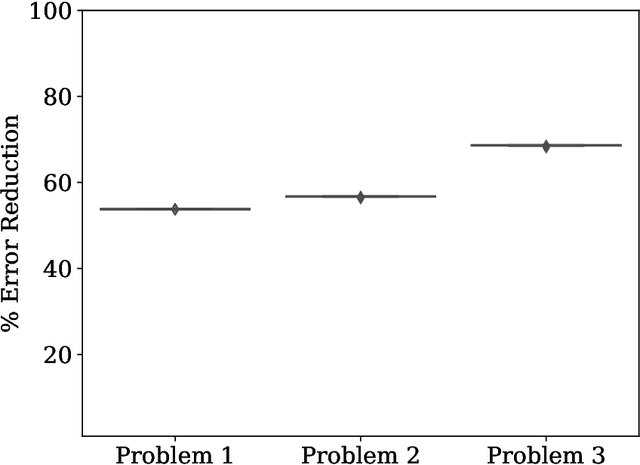
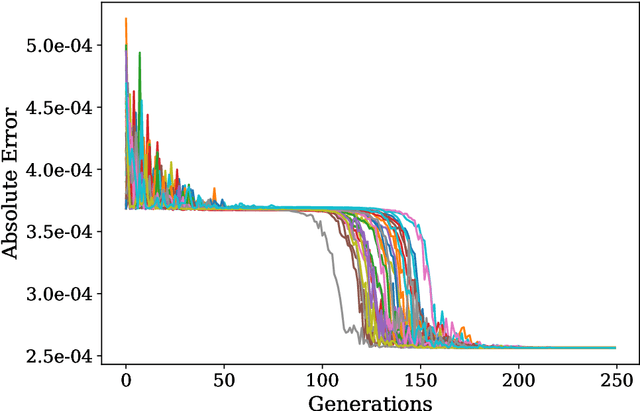
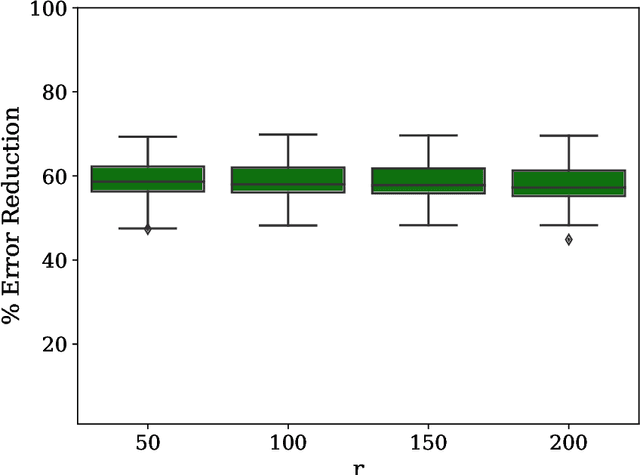
One of the most promising applications of near-term quantum computing is the simulation of quantum systems, a classically intractable task. Quantum simulation requires computationally expensive matrix exponentiation; Trotter-Suzuki decomposition of this exponentiation enables efficient simulation to a desired accuracy on a quantum computer. We apply the Covariance Matrix Adaptation Evolutionary Strategy (CMA-ES) algorithm to optimise the Trotter-Suzuki decompositions of a canonical quantum system, the Heisenberg Chain; we reduce simulation error by around 60%. We introduce this problem to the computational search community, show that an evolutionary optimisation approach is robust across runs and problem instances, and find that optimisation results generalise to the simulation of larger systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge