Fine-tune your Classifier: Finding Correlations With Temperature

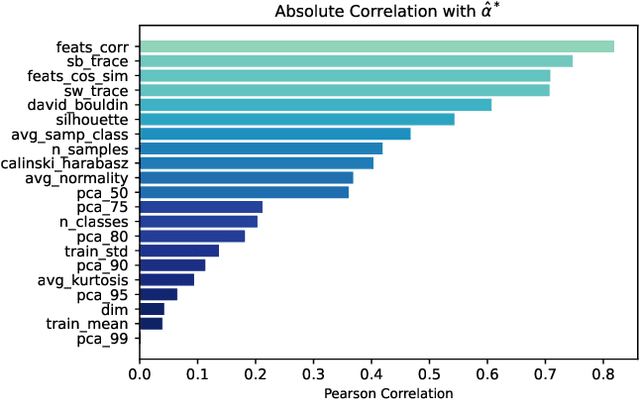
Temperature is a widely used hyperparameter in various tasks involving neural networks, such as classification or metric learning, whose choice can have a direct impact on the model performance. Most of existing works select its value using hyperparameter optimization methods requiring several runs to find the optimal value. We propose to analyze the impact of temperature on classification tasks by describing a dataset as a set of statistics computed on representations on which we can build a heuristic giving us a default value of temperature. We study the correlation between these extracted statistics and the observed optimal temperatures. This preliminary study on more than a hundred combinations of different datasets and features extractors highlights promising results towards the construction of a general heuristic for temperature.

What can we Learn by Predicting Accuracy?

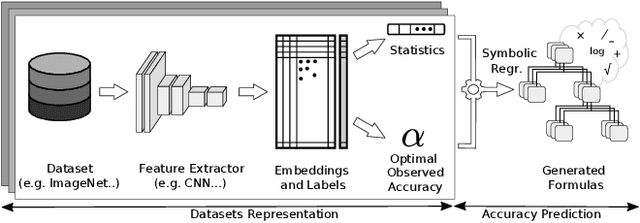
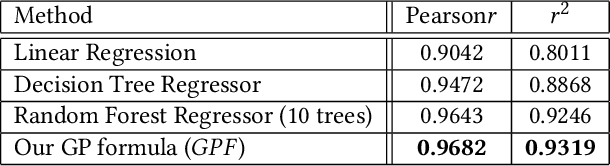
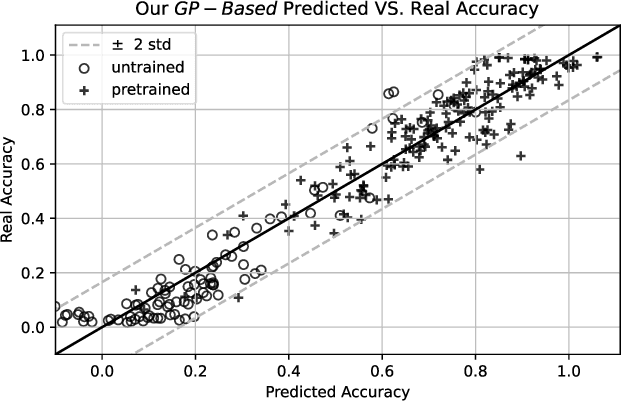
This paper seeks to answer the following question: "What can we learn by predicting accuracy?" Indeed, classification is one of the most popular task in machine learning and many loss functions have been developed to maximize this non-differentiable objective. Unlike past work on loss function design, which was mostly guided by intuition and theory before being validated by experimentation, here we propose to approach this problem in the opposite way : we seek to extract knowledge from experiments. This data-driven approach is similar to that used in physics to discover general laws from data. We used a symbolic regression method to automatically find a mathematical expression that is highly correlated with the accuracy of a linear classifier. The formula discovered on more than 260 datasets has a Pearson correlation of 0.96 and a r2 of 0.93. More interestingly, this formula is highly explainable and confirms insights from various previous papers on loss design. We hope this work will open new perspectives in the search for new heuristics leading to a deeper understanding of machine learning theory.