A Framework for Comparing Uncertain Inference Systems to Probability

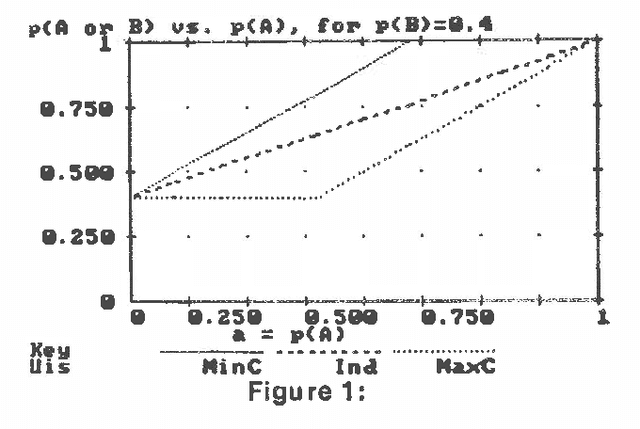
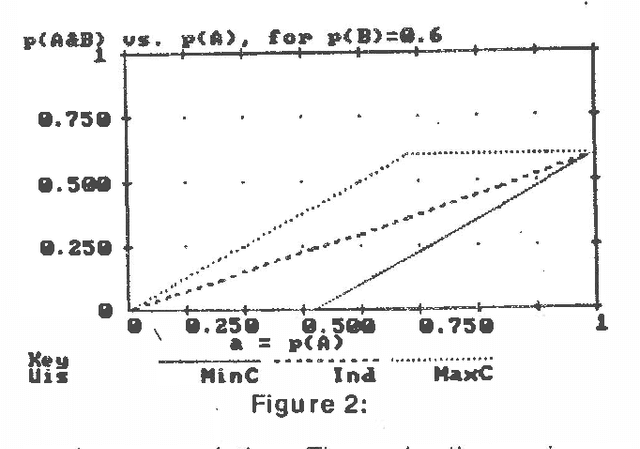
Several different uncertain inference systems (UISs) have been developed for representing uncertainty in rule-based expert systems. Some of these, such as Mycin's Certainty Factors, Prospector, and Bayes' Networks were designed as approximations to probability, and others, such as Fuzzy Set Theory and DempsterShafer Belief Functions were not. How different are these UISs in practice, and does it matter which you use? When combining and propagating uncertain information, each UIS must, at least by implication, make certain assumptions about correlations not explicily specified. The maximum entropy principle with minimum cross-entropy updating, provides a way of making assumptions about the missing specification that minimizes the additional information assumed, and thus offers a standard against which the other UISs can be compared. We describe a framework for the experimental comparison of the performance of different UISs, and provide some illustrative results.

Experimentally Comparing Uncertain Inference Systems to Probability

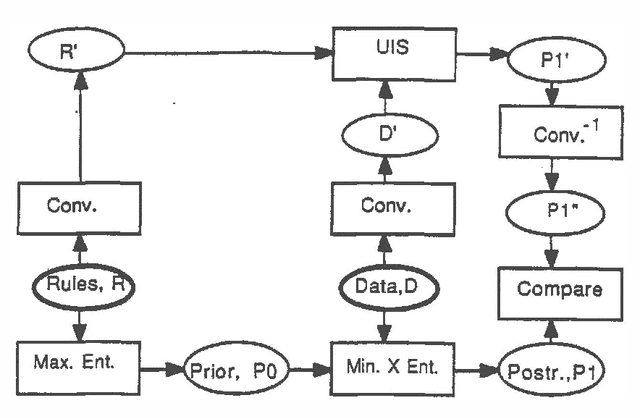
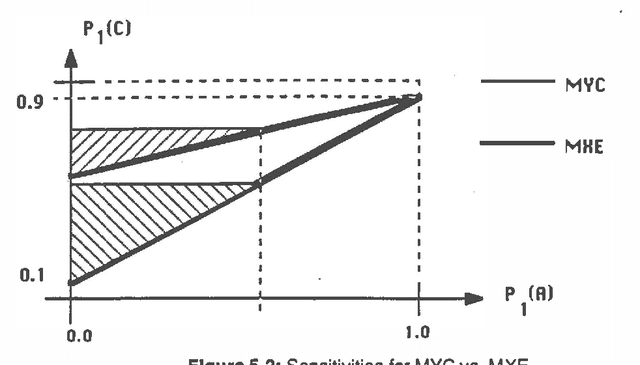
This paper examines the biases and performance of several uncertain inference systems: Mycin, a variant of Mycin. and a simplified version of probability using conditional independence assumptions. We present axiomatic arguments for using Minimum Cross Entropy inference as the best way to do uncertain inference. For Mycin and its variant we found special situations where its performance was very good, but also situations where performance was worse than random guessing, or where data was interpreted as having the opposite of its true import We have found that all three of these systems usually gave accurate results, and that the conditional independence assumptions gave the most robust results. We illustrate how the Importance of biases may be quantitatively assessed and ranked. Considerations of robustness might be a critical factor is selecting UlS's for a given application.

The Role of Tuning Uncertain Inference Systems

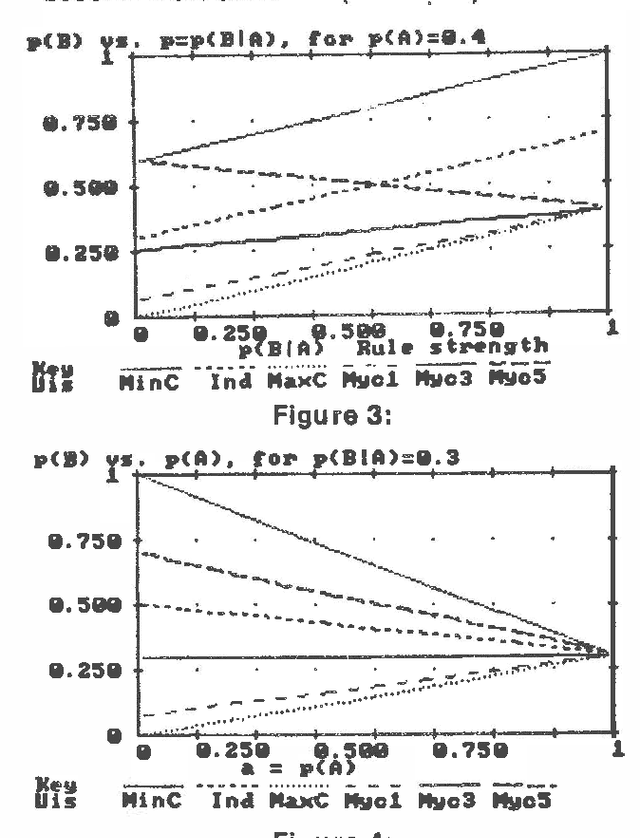
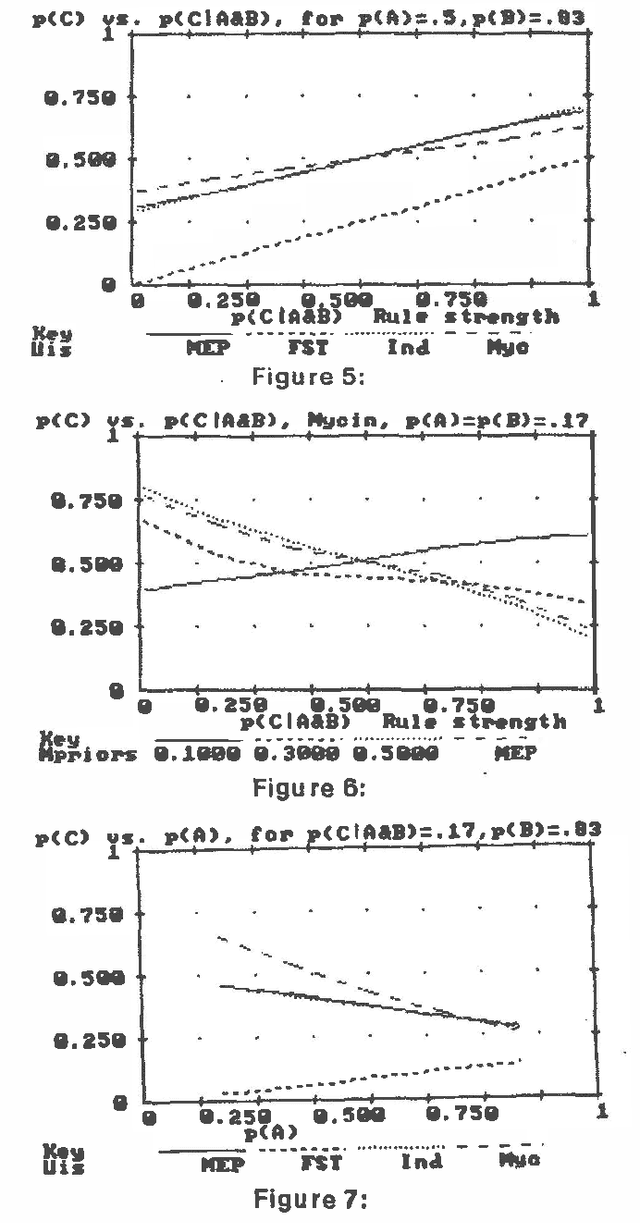
This study examined the effects of "tuning" the parameters of the incremental function of MYCIN, the independent function of PROSPECTOR, a probability model that assumes independence, and a simple additive linear equation. me parameters of each of these models were optimized to provide solutions which most nearly approximated those from a full probability model for a large set of simple networks. Surprisingly, MYCIN, PROSPECTOR, and the linear equation performed equivalently; the independence model was clearly more accurate on the networks studied.

Satisfaction of Assumptions is a Weak Predictor of Performance

This paper demonstrates a methodology for examining the accuracy of uncertain inference systems (UIS), after their parameters have been optimized, and does so for several common UIS's. This methodology may be used to test the accuracy when either the prior assumptions or updating formulae are not exactly satisfied. Surprisingly, these UIS's were revealed to be no more accurate on the average than a simple linear regression. Moreover, even on prior distributions which were deliberately biased so as give very good accuracy, they were less accurate than the simple probabilistic model which assumes marginal independence between inputs. This demonstrates that the importance of updating formulae can outweigh that of prior assumptions. Thus, when UIS's are judged by their final accuracy after optimization, we get completely different results than when they are judged by whether or not their prior assumptions are perfectly satisfied.