Data Complexity in Expressive Description Logics With Path Expressions

We investigate the data complexity of the satisfiability problem for the very expressive description logic ZOIQ (a.k.a. ALCHb Self reg OIQ) over quasi-forests and establish its NP-completeness. This completes the data complexity landscape for decidable fragments of ZOIQ, and reproves known results on decidable fragments of OWL2 (SR family). Using the same technique, we establish coNEXPTIME-completeness (w.r.t. the combined complexity) of the entailment problem of rooted queries in ZIQ.

Exploring Non-Regular Extensions of Propositional Dynamic Logic with Description-Logics Features

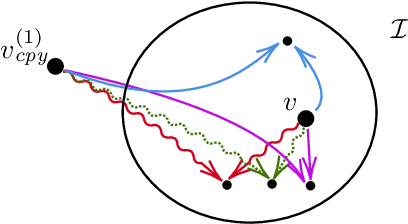
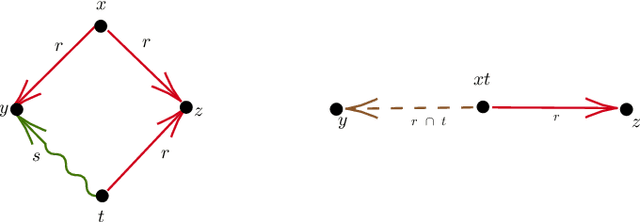
We investigate the impact of non-regular path expressions on the decidability of satisfiability checking and querying in description logics extending ALC. Our primary objects of interest are ALCreg and ALCvpl, the extensions of with path expressions employing, respectively, regular and visibly-pushdown languages. The first one, ALCreg, is a notational variant of the well-known Propositional Dynamic Logic of Fischer and Ladner. The second one, ALCvpl, was introduced and investigated by Loding and Serre in 2007. The logic ALCvpl generalises many known decidable non-regular extensions of ALCreg. We provide a series of undecidability results. First, we show that decidability of the concept satisfiability problem for ALCvpl is lost upon adding the seemingly innocent Self operator. Second, we establish undecidability for the concept satisfiability problem for ALCvpl extended with nominals. Interestingly, our undecidability proof relies only on one single non-regular (visibly-pushdown) language, namely on r#s# := { r^n s^n | n in N } for fixed role names r and s. Finally, in contrast to the classical database setting, we establish undecidability of query entailment for queries involving non-regular atoms from r#s#, already in the case of ALC-TBoxes.

Lutz's Spoiler Technique Revisited: A Unified Approach to Worst-Case Optimal Entailment of Unions of Conjunctive Queries in Locally-Forward Description Logics

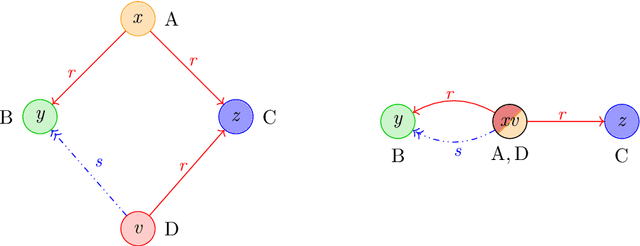
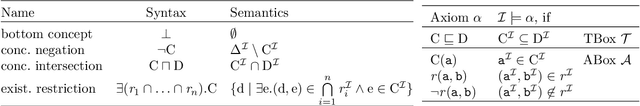
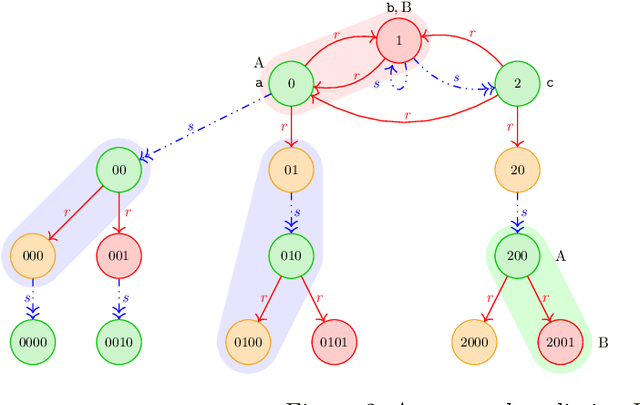
We present a unified approach to (both finite and unrestricted) worst-case optimal entailment of (unions of) conjunctive queries (U)CQs in the wide class of "locally-forward" description logics. The main technique that we employ is a generalisation of Lutz's spoiler technique, originally developed for CQ entailment in ALCHQ. Our result closes numerous gaps present in the literature, most notably implying ExpTime-completeness of (U)CQ-querying for any superlogic of ALC contained in ALCHbregQ, and, as we believe, is abstract enough to be employed as a black-box in many new scenarios.

The Price of Selfishness: Conjunctive Query Entailment for ALCSelf is 2ExpTime-hard

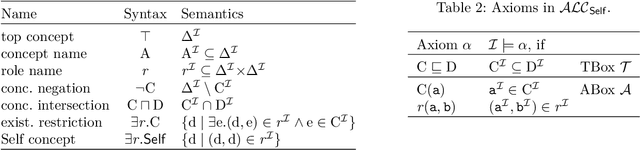
In logic-based knowledge representation, query answering has essentially replaced mere satisfiability checking as the inferencing problem of primary interest. For knowledge bases in the basic description logic ALC, the computational complexity of conjunctive query (CQ) answering is well known to be ExpTime-complete and hence not harder than satisfiability. This does not change when the logic is extended by certain features (such as counting or role hierarchies), whereas adding others (inverses, nominals or transitivity together with role-hierarchies) turns CQ answering exponentially harder. We contribute to this line of results by showing the surprising fact that even extending ALC by just the Self operator - which proved innocuous in many other contexts - increases the complexity of CQ entailment to 2ExpTime. As common for this type of problem, our proof establishes a reduction from alternating Turing machines running in exponential space, but several novel ideas and encoding tricks are required to make the approach work in that specific, restricted setting.

Satisfiability and Query Answering in Description Logics with Global and Local Cardinality Constraints

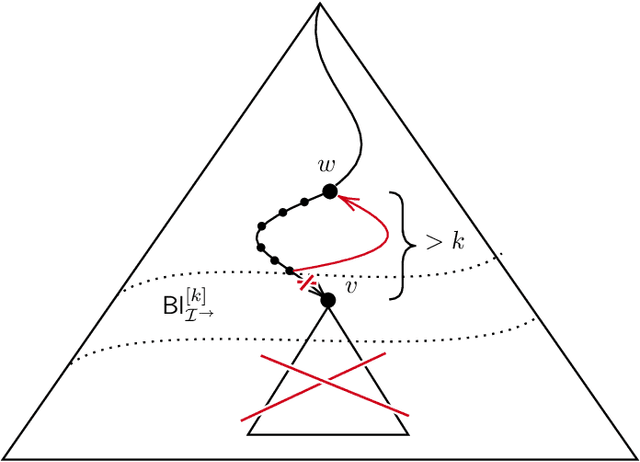
We introduce and investigate the expressive description logic (DL) ALCSCC++, in which the global and local cardinality constraints introduced in previous papers can be mixed. On the one hand, we prove that this does not increase the complexity of satisfiability checking and other standard inference problems. On the other hand, the satisfiability problem becomes undecidable if inverse roles are added to the languages. In addition, even without inverse roles, conjunctive query entailment in this DL turns out to be undecidable. We prove that decidability of querying can be regained if global and local constraints are not mixed and the global constraints are appropriately restricted. The latter result is based on a locally-acyclic model construction, and it reduces query entailment to ABox consistency in the restricted setting, i.e., to ABox consistency w.r.t. restricted cardinality constraints in ALCSCC, for which we can show an ExpTime upper bound.

Statistical EL is ExpTime-complete

We show that consistency of Statistical EL knowledge bases, as defined by Penaloza and Potyka in SUM 2017 [4] is ExpTime-hard. Together with the existing ExpTime upper bound by Baader in FroCos 2017 [1], the result leads to the ExpTime-completeness of the mentioned logic. Our proof goes via a reduction from consistency of EL extended with an atomic negation, which is known to be equivalent to the well-known ExpTime-complete description logic ALC.