The Price of Selfishness: Conjunctive Query Entailment for ALCSelf is 2ExpTime-hard
Paper and Code
Jun 29, 2021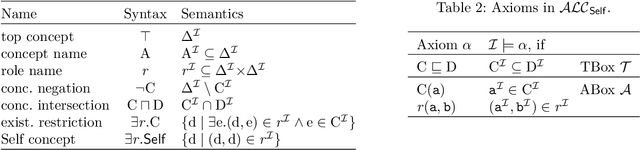
In logic-based knowledge representation, query answering has essentially replaced mere satisfiability checking as the inferencing problem of primary interest. For knowledge bases in the basic description logic ALC, the computational complexity of conjunctive query (CQ) answering is well known to be ExpTime-complete and hence not harder than satisfiability. This does not change when the logic is extended by certain features (such as counting or role hierarchies), whereas adding others (inverses, nominals or transitivity together with role-hierarchies) turns CQ answering exponentially harder. We contribute to this line of results by showing the surprising fact that even extending ALC by just the Self operator - which proved innocuous in many other contexts - increases the complexity of CQ entailment to 2ExpTime. As common for this type of problem, our proof establishes a reduction from alternating Turing machines running in exponential space, but several novel ideas and encoding tricks are required to make the approach work in that specific, restricted setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge