Particle gradient descent model for point process generation

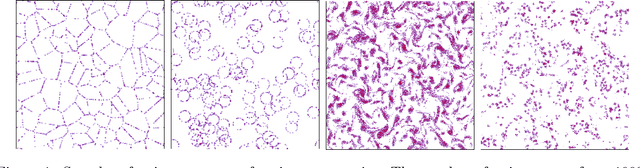
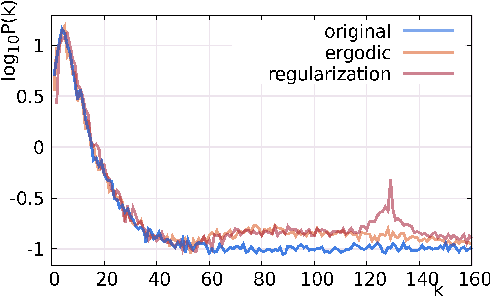
This paper introduces a generative model for planar point processes in a square window, built upon a single realization of a stationary, ergodic point process observed in this window. Inspired by recent advances in gradient descent methods for maximum entropy models, we propose a method to generate similar point patterns by jointly moving particles of an initial Poisson configuration towards a target counting measure. The target measure is generated via a deterministic gradient descent algorithm, so as to match a set of statistics of the given, observed realization. Our statistics are estimators of the multi-scale wavelet phase harmonic covariance, recently proposed in image modeling. They allow one to capture geometric structures through multi-scale interactions between wavelet coefficients. Both our statistics and the gradient descent algorithm scale better with the number of observed points than the classical k-nearest neighbour distances previously used in generative models for point processes, based on the rejection sampling or simulated-annealing. The overall quality of our model is evaluated on point processes with various geometric structures through spectral and topological data analysis.

Statistical learning of geometric characteristics of wireless networks

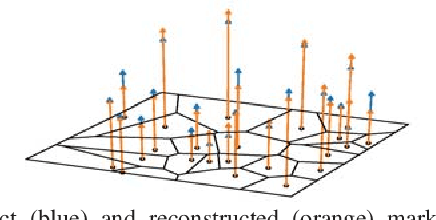
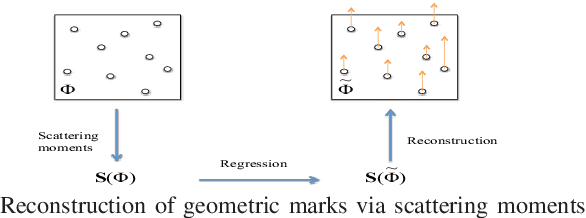
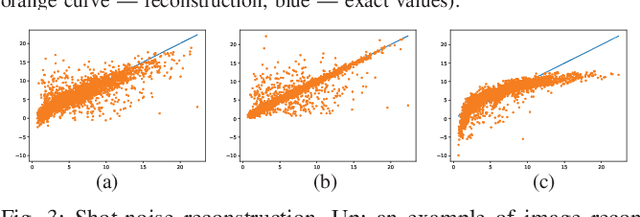
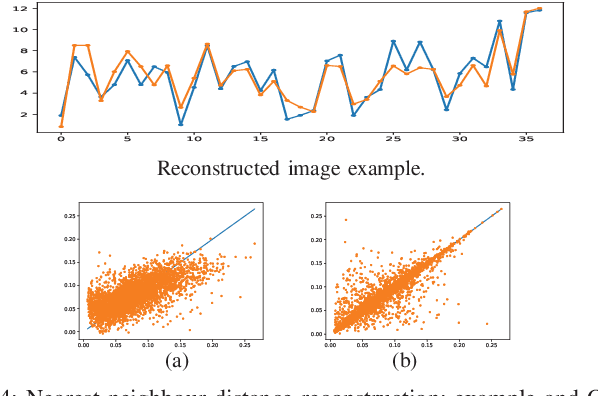
Motivated by the prediction of cell loads in cellular networks, we formulate the following new, fundamental problem of statistical learning of geometric marks of point processes: An unknown marking function, depending on the geometry of point patterns, produces characteristics (marks) of the points. One aims at learning this function from the examples of marked point patterns in order to predict the marks of new point patterns. To approximate (interpolate) the marking function, in our baseline approach, we build a statistical regression model of the marks with respect some local point distance representation. In a more advanced approach, we use a global data representation via the scattering moments of random measures, which build informative and stable to deformations data representation, already proven useful in image analysis and related application domains. In this case, the regression of the scattering moments of the marked point patterns with respect to the non-marked ones is combined with the numerical solution of the inverse problem, where the marks are recovered from the estimated scattering moments. Considering some simple, generic marks, often appearing in the modeling of wireless networks, such as the shot-noise values, nearest neighbour distance, and some characteristics of the Voronoi cells, we show that the scattering moments can capture similar geometry information as the baseline approach, and can reach even better performance, especially for non-local marking functions. Our results motivate further development of statistical learning tools for stochastic geometry and analysis of wireless networks, in particular to predict cell loads in cellular networks from the locations of base stations and traffic demand.

Determinantal thinning of point processes with network learning applications

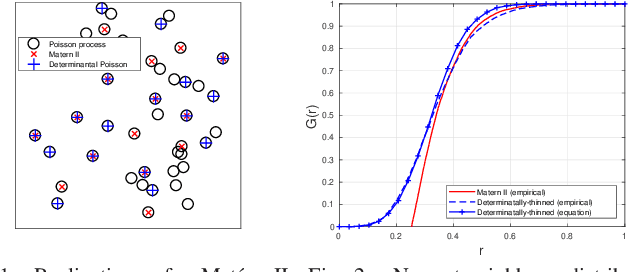
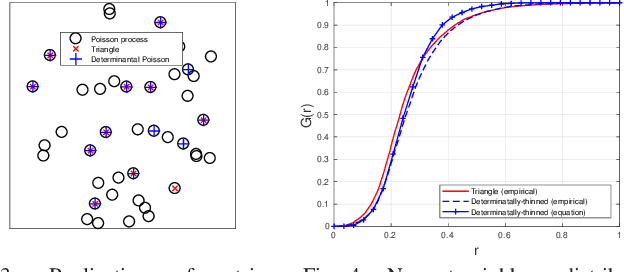
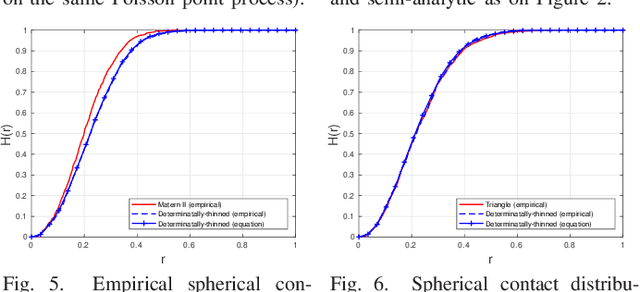
A new type of dependent thinning for point processes in continuous space is proposed, which leverages the advantages of determinantal point processes defined on finite spaces and, as such, is particularly amenable to statistical, numerical, and simulation techniques. It gives a new point process that can serve as a network model exhibiting repulsion. The properties and functions of the new point process, such as moment measures, the Laplace functional, the void probabilities, as well as conditional (Palm) characteristics can be estimated accurately by simulating the underlying (non-thinned) point process, which can be taken, for example, to be Poisson. This is in contrast (and preference to) finite Gibbs point processes, which, instead of thinning, require weighting the Poisson realizations, involving usually intractable normalizing constants. Models based on determinantal point processes are also well suited for statistical (supervised) learning techniques, allowing the models to be fitted to observed network patterns with some particular geometric properties. We illustrate this approach by imitating with determinantal thinning the well-known Mat{\'e}rn~II hard-core thinning, as well as a soft-core thinning depending on nearest-neighbour triangles. These two examples demonstrate how the proposed approach can lead to new, statistically optimized, probabilistic transmission scheduling schemes.