Paul Keeler
Determinantal thinning of point processes with network learning applications
Oct 09, 2018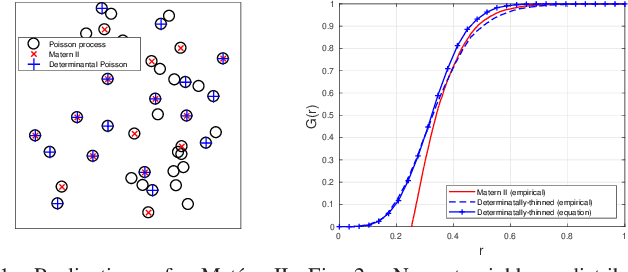
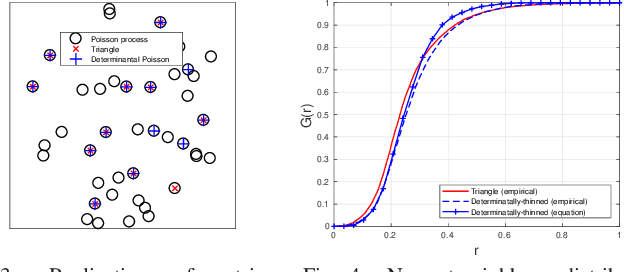
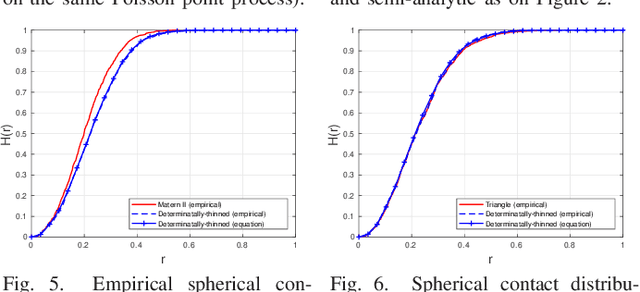
Abstract:A new type of dependent thinning for point processes in continuous space is proposed, which leverages the advantages of determinantal point processes defined on finite spaces and, as such, is particularly amenable to statistical, numerical, and simulation techniques. It gives a new point process that can serve as a network model exhibiting repulsion. The properties and functions of the new point process, such as moment measures, the Laplace functional, the void probabilities, as well as conditional (Palm) characteristics can be estimated accurately by simulating the underlying (non-thinned) point process, which can be taken, for example, to be Poisson. This is in contrast (and preference to) finite Gibbs point processes, which, instead of thinning, require weighting the Poisson realizations, involving usually intractable normalizing constants. Models based on determinantal point processes are also well suited for statistical (supervised) learning techniques, allowing the models to be fitted to observed network patterns with some particular geometric properties. We illustrate this approach by imitating with determinantal thinning the well-known Mat{\'e}rn~II hard-core thinning, as well as a soft-core thinning depending on nearest-neighbour triangles. These two examples demonstrate how the proposed approach can lead to new, statistically optimized, probabilistic transmission scheduling schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge