On the Scope of the Universal-Algebraic Approach to Constraint Satisfaction

The universal-algebraic approach has proved a powerful tool in the study of the complexity of CSPs. This approach has previously been applied to the study of CSPs with finite or (infinite) omega-categorical templates, and relies on two facts. The first is that in finite or omega-categorical structures A, a relation is primitive positive definable if and only if it is preserved by the polymorphisms of A. The second is that every finite or omega-categorical structure is homomorphically equivalent to a core structure. In this paper, we present generalizations of these facts to infinite structures that are not necessarily omega-categorical. (This abstract has been severely curtailed by the space constraints of arXiv -- please read the full abstract in the article.) Finally, we present applications of our general results to the description and analysis of the complexity of CSPs. In particular, we give general hardness criteria based on the absence of polymorphisms that depend on more than one argument, and we present a polymorphism-based description of those CSPs that are first-order definable (and therefore can be solved in polynomial time).

Containment, Equivalence and Coreness from CSP to QCSP and beyond

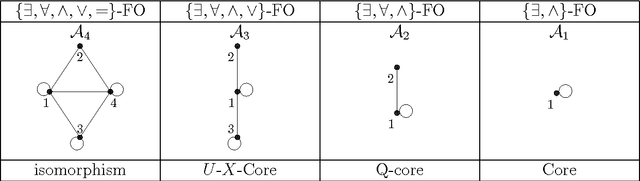
The constraint satisfaction problem (CSP) and its quantified extensions, whether without (QCSP) or with disjunction (QCSP_or), correspond naturally to the model checking problem for three increasingly stronger fragments of positive first-order logic. Their complexity is often studied when parameterised by a fixed model, the so-called template. It is a natural question to ask when two templates are equivalent, or more generally when one "contain" another, in the sense that a satisfied instance of the first will be necessarily satisfied in the second. One can also ask for a smallest possible equivalent template: this is known as the core for CSP. We recall and extend previous results on containment, equivalence and "coreness" for QCSP_or before initiating a preliminary study of cores for QCSP which we characterise for certain structures and which turns out to be more elusive.