Containment, Equivalence and Coreness from CSP to QCSP and beyond
Paper and Code
Apr 26, 2012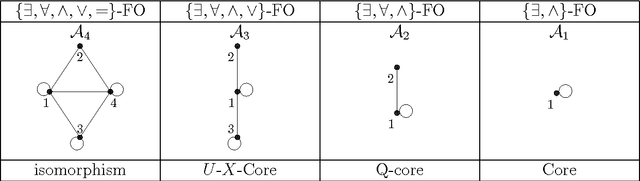
The constraint satisfaction problem (CSP) and its quantified extensions, whether without (QCSP) or with disjunction (QCSP_or), correspond naturally to the model checking problem for three increasingly stronger fragments of positive first-order logic. Their complexity is often studied when parameterised by a fixed model, the so-called template. It is a natural question to ask when two templates are equivalent, or more generally when one "contain" another, in the sense that a satisfied instance of the first will be necessarily satisfied in the second. One can also ask for a smallest possible equivalent template: this is known as the core for CSP. We recall and extend previous results on containment, equivalence and "coreness" for QCSP_or before initiating a preliminary study of cores for QCSP which we characterise for certain structures and which turns out to be more elusive.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge