Finite Sample Analysis of Distribution-Free Confidence Ellipsoids for Linear Regression

The least squares (LS) estimate is the archetypical solution of linear regression problems. The asymptotic Gaussianity of the scaled LS error is often used to construct approximate confidence ellipsoids around the LS estimate, however, for finite samples these ellipsoids do not come with strict guarantees, unless some strong assumptions are made on the noise distributions. The paper studies the distribution-free Sign-Perturbed Sums (SPS) ellipsoidal outer approximation (EOA) algorithm which can construct non-asymptotically guaranteed confidence ellipsoids under mild assumptions, such as independent and symmetric noise terms. These ellipsoids have the same center and orientation as the classical asymptotic ellipsoids, only their radii are different, which radii can be computed by convex optimization. Here, we establish high probability non-asymptotic upper bounds for the sizes of SPS outer ellipsoids for linear regression problems and show that the volumes of these ellipsoids decrease at the optimal rate. Finally, the difference between our theoretical bounds and the empirical sizes of the regions are investigated experimentally.

Data-Driven Upper Confidence Bounds with Near-Optimal Regret for Heavy-Tailed Bandits

Stochastic multi-armed bandits (MABs) provide a fundamental reinforcement learning model to study sequential decision making in uncertain environments. The upper confidence bounds (UCB) algorithm gave birth to the renaissance of bandit algorithms, as it achieves near-optimal regret rates under various moment assumptions. Up until recently most UCB methods relied on concentration inequalities leading to confidence bounds which depend on moment parameters, such as the variance proxy, that are usually unknown in practice. In this paper, we propose a new distribution-free, data-driven UCB algorithm for symmetric reward distributions, which needs no moment information. The key idea is to combine a refined, one-sided version of the recently developed resampled median-of-means (RMM) method with UCB. We prove a near-optimal regret bound for the proposed anytime, parameter-free RMM-UCB method, even for heavy-tailed distributions.

Finite-Sample Identification of Linear Regression Models with Residual-Permuted Sums

This letter studies a distribution-free, finite-sample data perturbation (DP) method, the Residual-Permuted Sums (RPS), which is an alternative of the Sign-Perturbed Sums (SPS) algorithm, to construct confidence regions. While SPS assumes independent (but potentially time-varying) noise terms which are symmetric about zero, RPS gets rid of the symmetricity assumption, but assumes i.i.d. noises. The main idea is that RPS permutes the residuals instead of perturbing their signs. This letter introduces RPS in a flexible way, which allows various design-choices. RPS has exact finite sample coverage probabilities and we provide the first proof that these permutation-based confidence regions are uniformly strongly consistent under general assumptions. This means that the RPS regions almost surely shrink around the true parameters as the sample size increases. The ellipsoidal outer-approximation (EOA) of SPS is also extended to RPS, and the effectiveness of RPS is validated by numerical experiments, as well.

Improving Kernel-Based Nonasymptotic Simultaneous Confidence Bands

The paper studies the problem of constructing nonparametric simultaneous confidence bands with nonasymptotic and distribition-free guarantees. The target function is assumed to be band-limited and the approach is based on the theory of Paley-Wiener reproducing kernel Hilbert spaces. The starting point of the paper is a recently developed algorithm to which we propose three types of improvements. First, we relax the assumptions on the noises by replacing the symmetricity assumption with a weaker distributional invariance principle. Then, we propose a more efficient way to estimate the norm of the target function, and finally we enhance the construction of the confidence bands by tightening the constraints of the underlying convex optimization problems. The refinements are also illustrated through numerical experiments.

Sample Complexity of the Sign-Perturbed Sums Identification Method: Scalar Case

Sign-Perturbed Sum (SPS) is a powerful finite-sample system identification algorithm which can construct confidence regions for the true data generating system with exact coverage probabilities, for any finite sample size. SPS was developed in a series of papers and it has a wide range of applications, from general linear systems, even in a closed-loop setup, to nonlinear and nonparametric approaches. Although several theoretical properties of SPS were proven in the literature, the sample complexity of the method was not analysed so far. This paper aims to fill this gap and provides the first results on the sample complexity of SPS. Here, we focus on scalar linear regression problems, that is we study the behaviour of SPS confidence intervals. We provide high probability upper bounds, under three different sets of assumptions, showing that the sizes of SPS confidence intervals shrink at a geometric rate around the true parameter, if the observation noises are subgaussian. We also show that similar bounds hold for the previously proposed outer approximation of the confidence region. Finally, we present simulation experiments comparing the theoretical and the empirical convergence rates.

On rate-optimal classification from non-private and from private data

In this paper we revisit the classical problem of classification, but impose privacy constraints. Under such constraints, the raw data $(X_1,Y_1),\ldots,(X_n,Y_n)$ cannot be directly observed, and all classifiers are functions of the randomised outcome of a suitable local differential privacy mechanism. The statistician is free to choose the form of this privacy mechanism, and here we add Laplace distributed noise to a discretisation of the location of each feature vector $X_i$ and to its label $Y_i$. The classification rule is the privatized version of the well-studied partitioning classification rule. In addition to the standard Lipschitz and margin conditions, a novel characteristic is introduced, by which the exact rate of convergence of the classification error probability is calculated, both for non-private and private data.

Distribution-Free Inference for the Regression Function of Binary Classification

One of the key objects of binary classification is the regression function, i.e., the conditional expectation of the class labels given the inputs. With the regression function not only a Bayes optimal classifier can be defined, but it also encodes the corresponding misclassification probabilities. The paper presents a resampling framework to construct exact, distribution-free and non-asymptotically guaranteed confidence regions for the true regression function for any user-chosen confidence level. Then, specific algorithms are suggested to demonstrate the framework. It is proved that the constructed confidence regions are strongly consistent, that is, any false model is excluded in the long run with probability one. The exclusion is quantified with probably approximately correct type bounds, as well. Finally, the algorithms are validated via numerical experiments, and the methods are compared to approximate asymptotic confidence ellipsoids.

Robust Independence Tests with Finite Sample Guarantees for Synchronous Stochastic Linear Systems

The paper introduces robust independence tests with non-asymptotically guaranteed significance levels for stochastic linear time-invariant systems, assuming that the observed outputs are synchronous, which means that the systems are driven by jointly i.i.d. noises. Our method provides bounds for the type I error probabilities that are distribution-free, i.e., the innovations can have arbitrary distributions. The algorithm combines confidence region estimates with permutation tests and general dependence measures, such as the Hilbert-Schmidt independence criterion and the distance covariance, to detect any nonlinear dependence between the observed systems. We also prove the consistency of our hypothesis tests under mild assumptions and demonstrate the ideas through the example of autoregressive systems.

Recursive Estimation of Conditional Kernel Mean Embeddings

Kernel mean embeddings, a widely used technique in machine learning, map probability distributions to elements of a reproducing kernel Hilbert space (RKHS). For supervised learning problems, where input-output pairs are observed, the conditional distribution of outputs given the inputs is a key object. The input dependent conditional distribution of an output can be encoded with an RKHS valued function, the conditional kernel mean map. In this paper we present a new recursive algorithm to estimate the conditional kernel mean map in a Hilbert space valued $L_2$ space, that is in a Bochner space. We prove the weak and strong $L_2$ consistency of our recursive estimator under mild conditions. The idea is to generalize Stone's theorem for Hilbert space valued regression in a locally compact Polish space. We present new insights about conditional kernel mean embeddings and give strong asymptotic bounds regarding the convergence of the proposed recursive method. Finally, the results are demonstrated on three application domains: for inputs coming from Euclidean spaces, Riemannian manifolds and locally compact subsets of function spaces.

Nonparametric, Nonasymptotic Confidence Bands with Paley-Wiener Kernels for Band-Limited Functions

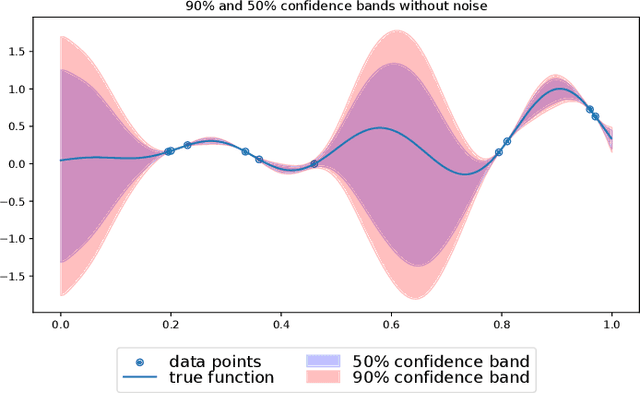
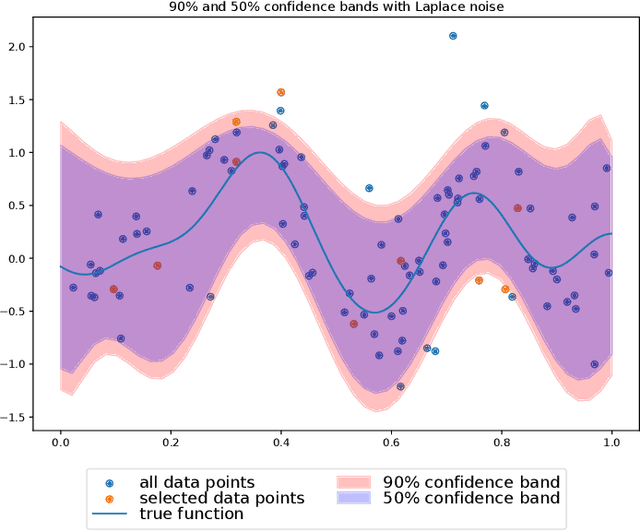
The paper introduces a method to construct confidence bands for bounded, band-limited functions based on a finite sample of input-output pairs. The approach is distribution-free w.r.t. the observation noises and only the knowledge of the input distribution is assumed. It is nonparametric, that is, it does not require a parametric model of the regression function and the regions have non-asymptotic guarantees. The algorithm is based on the theory of Paley-Wiener reproducing kernel Hilbert spaces. The paper first studies the fully observable variant, when there are no noises on the observations and only the inputs are random; then it generalizes the ideas to the noisy case using gradient-perturbation methods. Finally, numerical experiments demonstrating both cases are presented.