Improving Kernel-Based Nonasymptotic Simultaneous Confidence Bands

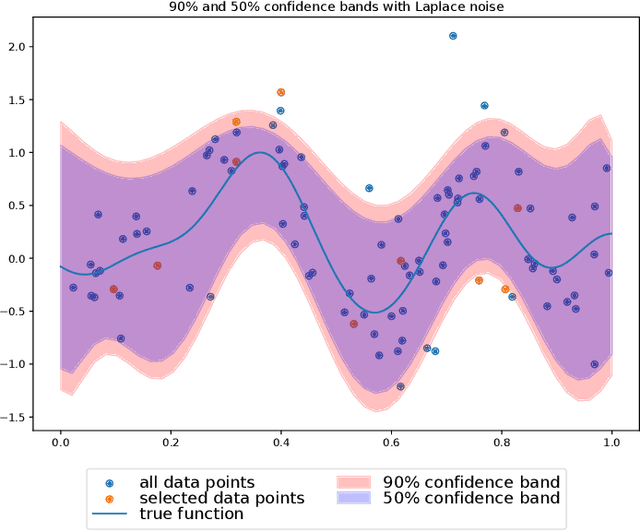
The paper studies the problem of constructing nonparametric simultaneous confidence bands with nonasymptotic and distribition-free guarantees. The target function is assumed to be band-limited and the approach is based on the theory of Paley-Wiener reproducing kernel Hilbert spaces. The starting point of the paper is a recently developed algorithm to which we propose three types of improvements. First, we relax the assumptions on the noises by replacing the symmetricity assumption with a weaker distributional invariance principle. Then, we propose a more efficient way to estimate the norm of the target function, and finally we enhance the construction of the confidence bands by tightening the constraints of the underlying convex optimization problems. The refinements are also illustrated through numerical experiments.

Nonparametric, Nonasymptotic Confidence Bands with Paley-Wiener Kernels for Band-Limited Functions

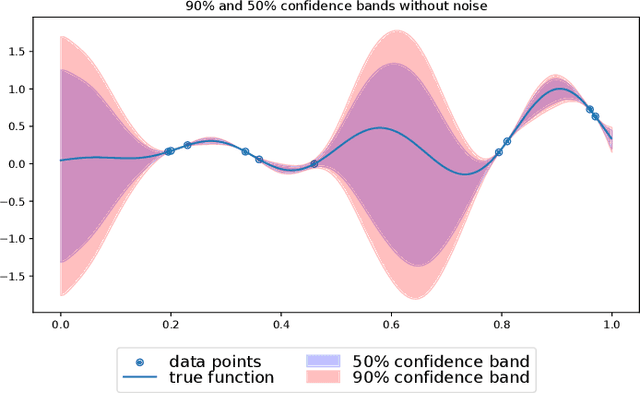
The paper introduces a method to construct confidence bands for bounded, band-limited functions based on a finite sample of input-output pairs. The approach is distribution-free w.r.t. the observation noises and only the knowledge of the input distribution is assumed. It is nonparametric, that is, it does not require a parametric model of the regression function and the regions have non-asymptotic guarantees. The algorithm is based on the theory of Paley-Wiener reproducing kernel Hilbert spaces. The paper first studies the fully observable variant, when there are no noises on the observations and only the inputs are random; then it generalizes the ideas to the noisy case using gradient-perturbation methods. Finally, numerical experiments demonstrating both cases are presented.