On the Implicit Bias of Gradient Descent for Temporal Extrapolation

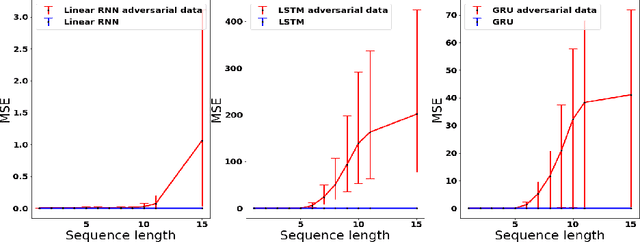
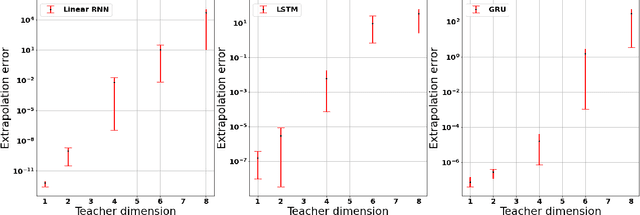
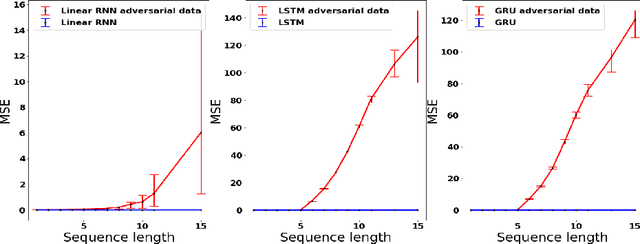
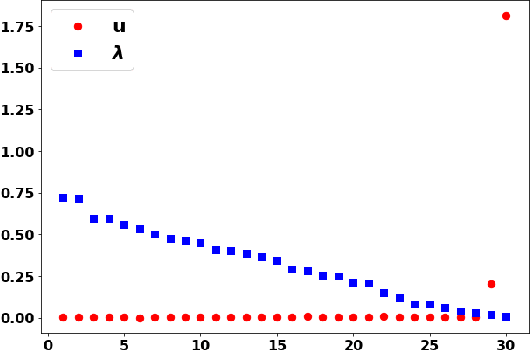
Common practice when using recurrent neural networks (RNNs) is to apply a model to sequences longer than those seen in training. This "extrapolating" usage deviates from the traditional statistical learning setup where guarantees are provided under the assumption that train and test distributions are identical. Here we set out to understand when RNNs can extrapolate, focusing on a simple case where the data generating distribution is memoryless. We first show that even with infinite training data, there exist RNN models that interpolate perfectly (i.e., they fit the training data) yet extrapolate poorly to longer sequences. We then show that if gradient descent is used for training, learning will converge to perfect extrapolation under certain assumption on initialization. Our results complement recent studies on the implicit bias of gradient descent, showing that it plays a key role in extrapolation when learning temporal prediction models.

Regularizing Towards Permutation Invariance in Recurrent Models

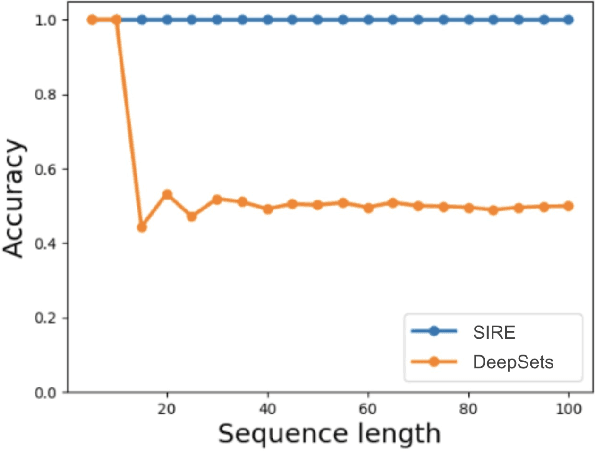
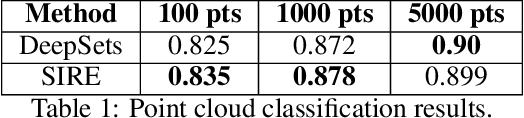
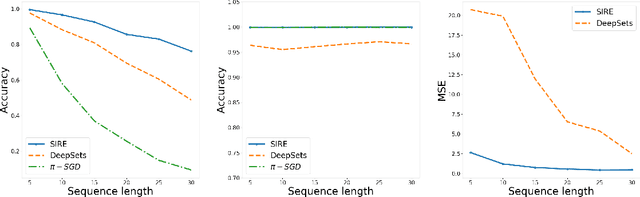
In many machine learning problems the output should not depend on the order of the input. Such "permutation invariant" functions have been studied extensively recently. Here we argue that temporal architectures such as RNNs are highly relevant for such problems, despite the inherent dependence of RNNs on order. We show that RNNs can be regularized towards permutation invariance, and that this can result in compact models, as compared to non-recurrent architectures. We implement this idea via a novel form of stochastic regularization. Existing solutions mostly suggest restricting the learning problem to hypothesis classes which are permutation invariant by design. Our approach of enforcing permutation invariance via regularization gives rise to models which are \textit{semi permutation invariant} (e.g. invariant to some permutations and not to others). We show that our method outperforms other permutation invariant approaches on synthetic and real world datasets.