Ashwin Machanavajjhala
Capacity Bounded Differential Privacy
Jul 03, 2019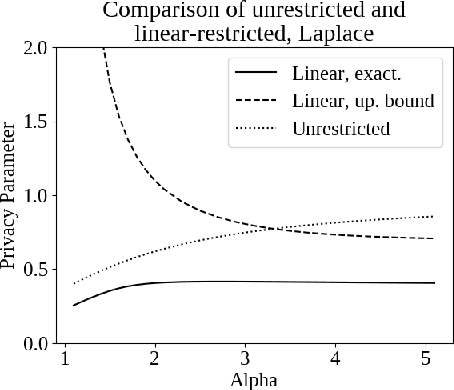
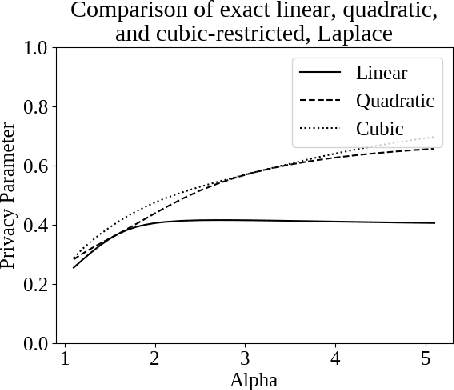
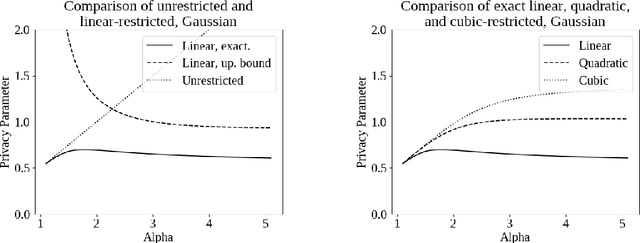
Abstract:Differential privacy, a notion of algorithmic stability, is a gold standard for measuring the additional risk an algorithm's output poses to the privacy of a single record in the dataset. Differential privacy is defined as the distance between the output distribution of an algorithm on neighboring datasets that differ in one entry. In this work, we present a novel relaxation of differential privacy, capacity bounded differential privacy, where the adversary that distinguishes output distributions is assumed to be capacity-bounded -- i.e. bounded not in computational power, but in terms of the function class from which their attack algorithm is drawn. We model adversaries in terms of restricted f-divergences between probability distributions, and study properties of the definition and algorithms that satisfy them.
Differentially Private Algorithms for Empirical Machine Learning
Nov 21, 2014

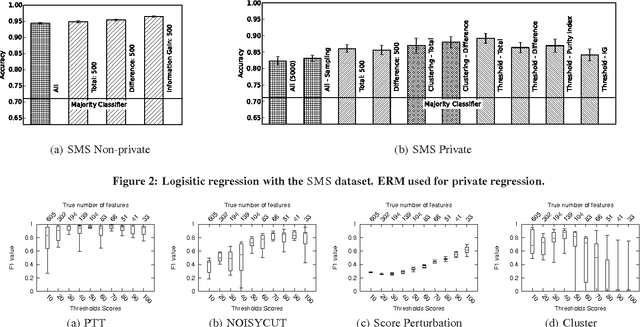
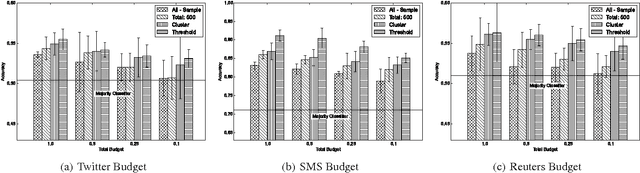
Abstract:An important use of private data is to build machine learning classifiers. While there is a burgeoning literature on differentially private classification algorithms, we find that they are not practical in real applications due to two reasons. First, existing differentially private classifiers provide poor accuracy on real world datasets. Second, there is no known differentially private algorithm for empirically evaluating the private classifier on a private test dataset. In this paper, we develop differentially private algorithms that mirror real world empirical machine learning workflows. We consider the private classifier training algorithm as a blackbox. We present private algorithms for selecting features that are input to the classifier. Though adding a preprocessing step takes away some of the privacy budget from the actual classification process (thus potentially making it noisier and less accurate), we show that our novel preprocessing techniques significantly increase classifier accuracy on three real-world datasets. We also present the first private algorithms for empirically constructing receiver operating characteristic (ROC) curves on a private test set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge